Прежде чем ознакомиться с нашим проектом, мы предлагаем Вам посмотреть тизер: https://www.powtoon.com/s/fFJqXsWucwu/1/m/s
Тема проекта: Секта чисел. Теорема Пифагора.
Творческое название проекта: Пифагоровы тайны: разгадка секты чисел.
Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах.
Причина такой популярности теоремы Пифагора это её простота, красота, значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы , свидетельствует о её широком применении, однако не все знают о нём. Именно поэтому тема исследования «Пифагоровы тайны: разгадка секты чисел» является актуальной.
Цель исследования: выяснить, в чем сущность взаимосвязи между теоремой Пифагора, теорией чисел и их влияние на различные области, раскрывая тайны пифагорейской секты чисел.
Гипотеза исследования: Пифагорейская секта чисел имеет глубокое влияние на развитие математики, науки и искусства, и их открытия и идеи продолжают влиять на современные исследования и инновации.
Задачи исследования:
- Провести углубленный анализ теоремы Пифагора и ее применений.
- Изучить вклад пифагорейской секты в теорию чисел.
- Исследовать связи между математикой и другими областями (музыка, архитектура, естественные науки).
- Создать визуальное представление результатов.
Методы исследования: работа с информационными источниками: анализ выбранной литературы и Интернет ресурсов; проведение опроса; анализ и обобщение статистических данных.
План исследования:
«Теорема Пифагора» — одна из наиболее фундаментальных теорем в геометрии, устанавливающая связь между длинами сторон прямоугольного треугольника. Эта теорема на протяжении веков оказывала значительное влияние на развитие математики и продолжает быть актуальной и в наши дни. Давайте совершим экскурс в историю и проследим ключевые события, связанные с теоремой Пифагора, в нашей ленте времени:
Пифагорейская секта, также известная как пифагорейская школа, была философской и религиозной общиной, основанной Пифагором в VI веке до н.э. в Кротоне, Италия. Эта община была известна не только своими математическими и философскими исследованиями, но и строгим образом жизни, который включал в себя различные аскетические практики и ритуалы. Пифагорейцы верили в переселение душ и придерживались вегетарианства. Они также придавали большое значение изучению математики, музыки и астрономии, видя в них путь к пониманию гармонии и порядка во Вселенной.
Теория чисел — это раздел математики, посвященный изучению свойств целых чисел и других целых чисел (например, рациональных чисел). Теория чисел включает в себя различные темы, такие как: делимость, свойства чисел, простые числа, диофантовы уравнения.
Пифагорейская школа, основанная Пифагором в VI веке до н.э., внесла существенный вклад в развитие теории чисел. Рассмотрим подробнее вклад Пифагорейской секты чисел в теорию чисел. Для этого предлагаем вам ознакомиться с презентацией:
https://prezi.com/view/FPGcsj0GWiV5V77UQY6V/?referral_token=cNyVXNlnB3FN
Ниже представлены ключевые достижения пифагорейцев с соответствующими определениями:
- Чётные и нечётные числа. Пифагорейцы различали чётные и нечётные числа.
- Чётное число- целое число, которое делится на 2, т.е. n=2k, где k — целое число.
- Нечётное число- целое число, не делящееся на 2, т.е. n=2k+1, где k — целое число.
- Совершенные числа. Изучали совершенные числа, представляющие особый интерес в теории чисел.
- Совершенное число- положительное целое число, равное сумме своих собственных делителей (положительных делителей, отличных от самого числа). Например, 28 является совершенным, так как 28=1+2+4+7+14.
- Пифагоровы тройки. Пифагорейцы открыли и классифицировали пифагоровы тройки.
- Пифагорова тройка- тройка целых чисел a, b и c, таких, что a2+b2=c Примеры включают (3,4,5) и (5,12,13).
- Иррациональные числа. Открытие существования иррациональных чисел, вероятно, членами пифагорейской школы, расширило концепцию числа за пределы рациональных чисел.
- Иррациональное число- действительное число, которое не может быть представлено в виде отношения nm, где m — целое число, а n — натуральное число. Примером иррационального числа является 2.
- Фигуративные числа(многие из которых были классифицированы и изучены пифагорейцами).
- Фигуративные числа- числа, которые можно представить геометрически. Подкатегории включают:
- Треугольные числа: Tn=2n(n+1), представляющие количество точек, образующих равносторонний треугольник.
- Квадратные числа: Sn=n2, представляющие количество точек, образующих квадрат.
Вклад пифагорейской школы не только расширил знания того времени о числах и их свойствах, но и заложил фундамент для дальнейших исследований в этой области, изменив понимание чисел и их роли в геометрии и других математических дисциплинах. Математика является фундаментальной наукой, которая имеет тесные связи с различными областями знаний.
О значительном вкладе пифагорейской секты в теорию чисел, её тесной связи с современной жизнью и заинтересованностью в ней, говорят нам результаты, проведенного опроса:
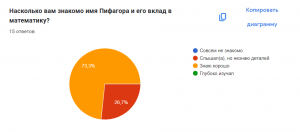
Анализ результатов опроса показал, что 73.5% опрошенных хорошо знакомы с именем Пифагора:
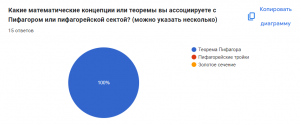
Все 15 участников опроса ассоциируют Пифагора или пифагорейскую секту с Теоремой Пифагора
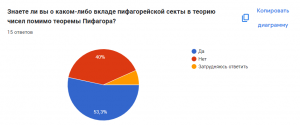
Большинство участников опроса имеют представление о кладе пифагорейской секты в теорию чисел помимо теорему Пифагора. Однако значительная доля участников не обладает такими знаниями, что подчеркивает необходимость дальнейшего образования или информирования в этой области.
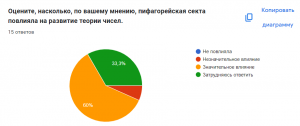
53,3% опрошенных признают значительное влияние пифагорейской секты на развитие теории чисел. При этом 40% участников затруднилась с оценкой, а мнение о незначительном влиянии практически отсутствует.
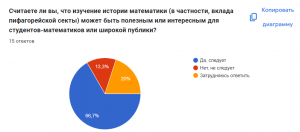
60% участников опроса поддерживают идею о том, что изучение истории математики и вклада пифагорейской секты может быть полезным или интересным как для студентов-математиков, так и для широкой публики.большинство опрошенных поддерживают изучение истории математики и считают его полезным или интересным. В то же время некоторая часть участников либо затруднилась с ответом, либо не видит в этом смысла.
В целом, результаты анализа диаграмм демонстрируют, что теорема Пифагора и пифагорейская секта остаются важными и влиятельными в современном восприятии математики и ее истории. Поддержка изучения истории математики среди опрошенных указывает на потенциальные возможности для развития образовательных программ и проектов по популяризации математических знаний.
ВЫВОД
В ходе работы над проектом было проведено комплексное исследование, позволившее достичь поставленной цели и подтвердить выдвинутую гипотезу. Результаты работы можно сформулировать следующим образом:
Цель исследования – выяснить сущность взаимосвязи между теоремой Пифагора, теорией чисел и их влиянием на различные области – была успешно достигнута. Установлено, что эта взаимосвязь заключается в том, что знаменитая теорема Пифагора является не просто изолированной геометрической формулой, а наглядным проявлением глобальной пифагорейской философии «всё есть число». Пифагорейцы видели в числовых соотношениях основу гармонии Вселенной, и их теорема стала одним из ключевых доказательств этой идеи.
Гипотеза исследования о том, что пифагорейская секта чисел оказала глубокое и продолжительное влияние на развитие математики, науки и искусства, которое сохраняется и сегодня, нашла свое полное подтверждение.
Для достижения цели и проверки гипотезы были последовательно решены следующие задачи:
1. Анализ теоремы Пифагора. В рамках первой задачи был проведен углубленный анализ теоремы. Было установлено, что её значение выходит далеко за рамки геометрии. Она применяется в физике, навигации, строительстве и даже в современных компьютерных технологиях, что доказывает её непреходящую практическую ценность.
2. Вклад в теорию чисел. Изучение вклада пифагорейцев в теорию чисел показало, что они заложили основы этой дисциплины. Они классифицировали числа (четные, нечетные, простые, совершенные), изучали пропорции и средние величины. Их открытие иррациональных чисел, хоть и стало кризисом для их учения, в итоге дало мощный толчок развитию математики.
3. Связи с другими областями. Исследование связей математики с другими сферами выявило, что пифагорейцы первыми установили числовые законы в музыке, связав гармоничные интервалы с простыми соотношениями (1:2, 2:3). Эти же принципы пропорций они перенесли в архитектуру для создания гармоничных зданий. Их учение о «гармонии сфер» повлияло на развитие астрономии и космологии.
4. Визуализация результатов. Для наглядного представления полученных данных была создана презентация, которая демонстрирует разветвленное влияние пифагорейского учения – от знаменитой теоремы до её проявлений в искусстве, науке и современных технологиях.
Таким образом, проект доказывает, что наследие «секты чисел» – это не просто одна теорема, а целостная философская система, которая впервые поставила число в центр мироздания и заложила основы для научного метода познания мира, актуального и по сей день.
Используемые источники
- Бондаренко Н.К. История математики: учебное пособие. – М.: Юрайт, 2023.
- Клайн М. Математика: Потеря́ное время (The World of Mathematics). – М.: Мир, 1977.
- Бучштбергер Б. Математика с увлечением: в двух книгах. Книга 1. – М.: Мир, 1987.
- Реале Дж. Западная философия от истоков до наших дней. Античность. – М.: Академический Проект, 2003.
- Глейзер Г.И. История математики в школе. – М.: Просвещение, 1974.
- Энтин М.А. Введение в историю математики. – М.: Учпедгиз, 1950.
- Pythagoras. Britannica. https://www.britannica.com/biography/Pythagoras
- Pythagoreanism. Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/pythagoreanism/
- Раздел «Пифагор и его школа» на портале «Элементы». https://elementy.ru
- Фигурнов Г.И. Теорема Пифагора и её доказательства. // Квант, №2, 1981.