Тема исследования: Число е
Цель исследования: исследовать историю числа е и расширить знания об этом иррациональном числе
Гипотеза исследования: Число е тайно присутствует в нашей жизни
Задачи исследования:
- изучить литературу с целью получения информации об истории числа е;
- выяснить его приближенное значение;
- рассмотреть различные способы определения числа е;
- рассмотреть решение задачи практического содержания проявления числа е в реальной жизни.
Методы исследования:
- изучение
- анализ
- опрос
История
Число е – это основание натуральных логарифмов и важнейшая математическая константа (обозначается строчной латинской буквой «e»), которая в высшей математике встречается буквально на каждом шагу, она играет особенно важную роль в дифференциальном и интегральном исчислении. Иногда число e называют числом Эйлера. Именно Эйлер первым ввел символ е (с этой буквы начинается его фамилия – Euler) и сделал так много открытий, связанных с числом е, что, в конце концов, е стали называть числом Эйлера. Численное значение указанного числа следующее:
e = 2,7 1828 1828 459045235360287471352662497757…,
Число е – трансцендентное число (доказал Ш. Эрмит в 1873 г.), то есть оно не является корнем никакого многочлена с целыми коэффициентами, и не существует закона, по которому чередуются цифры после запятой в значении числа е (ещё в 1961 г. с помощью ЭВМ было получено 100265 десятичных знаков). Предполагается, что e – это нормальное число, то есть вероятность появления разных цифр в его (бесконечной!) записи одинакова. Также e — основание натурального логарифма, математическая константа, иррациональное число.
Иногда число е малообоснованно называют неперовым числом, по имени изобретателя логарифмов Джона Непера (1550–1617).
Число е встречается буквально на каждом шагу в высшей математике, в особенности в задачах теории вероятностей, в реальной жизни оно проявляет себя ярче всего при росте какой – либо величины, будь то рост клетки или банковского счета.
Саму же константу впервые вычислил швейцарский математик Якоб Бернулли в ходе решения задачи о предельной величине процентного дохода. Он обнаружил, что если исходная сумма $1 { и начисляется 100 % годовых один раз в конце года, то итоговая сумма будет $2 Но если те же самые проценты начислять два раза в год, то $1 умножается на 1 , 5 дважды, получая $1 , 00 ⋅ 1 , 5 2 = $ 2 , 25. Начисления процентов раз в квартал приводит к $ 1 , 00 ⋅ 1 , 25 4 = $ 2,441 40625 , и так далее. Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента имеет предел: 
Таким образом, константа e означает максимально возможную годовую прибыль при 100 % годовых и максимальной частоте капитализации процентов.
Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.
Букву e начал использовать Эйлер в 1727 году, впервые она встречается в письме Эйлера немецкому математику Гольдбаху от 25 ноября 1731 года, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически», 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.
Применение числа e
В финансах
Число e широко используется в финансах для финансовых расчетов. Одним из наиболее распространенных применений е в финансах является расчет сложных процентов. Сложные проценты — это термин, который относится к процентам по кредиту или депозиту, рассчитываемым на основе как первоначально основной суммы, так и накопленных процентов.
Формулу сложных процентов можно представить следующим образом:
A = P * (1 + r/n)^(nt)
где A — конечная сумма, P — первоначальная основная сумма, r — процентная ставка, n — количество начислений процентов в год, t — количество лет.
Математическая константа e используется для представления числа, на которое начисляются проценты в год, а экспоненциальная функция позволяет нам рассчитать конечную сумму.
В финансах e также используется в моделях ценообразования опционов, таких как модель Блэка-Шоулза и биномиальная модель ценообразования опционов. В этих моделях e используется для расчета приведенной стоимости опциона с учетом временной стоимости денег и волатильности базового актива.
В дополнение к этим приложениям e также используется в расчетах аннуитетов, бессрочных и непредвиденных обстоятельств жизни. В целом число e играет жизненно важную роль в различных финансовых расчетах и моделях, обеспечивая последовательное и точное представление экспоненциального роста и стоимости денег во времени.
В физике и математике
Число e широко используется в физике и математике, поскольку оно фигурирует в различных математических формулах и моделях. Вот некоторые из его применений:
Экспоненциальные функции. В математике e является основанием натурального логарифма и используется для определения экспоненциальных функций. Показательная функция — одно из важнейших математических понятий, которое широко используется в различных областях науки, в том числе и в физике.
Непрерывные сложные проценты. В финансах буква «e» используется для расчета непрерывных сложных процентов, когда процентная ставка непрерывно начисляется с течением времени. В этой модели сумма процентов растет экспоненциально со временем.
Дифференциальные уравнения — e используется при решении дифференциальных уравнений, которые описывают, как величина изменяется во времени. Многие физические и биологические процессы описываются дифференциальными уравнениями, и e часто фигурирует в этих уравнениях как константа.
Теория вероятностей — e используется в теории вероятностей, где оно фигурирует в различных формулах, описывающих распределение вероятностей событий во времени. Например, экспоненциальное распределение, широко используемое в технике надежности, основано на e.
Квантовая механика — e также появляется в квантовой механике, где оно используется при решении уравнения Шрёдингера, описывающего поведение частиц на квантовом уровне. В квантовой механике e используется для описания экспоненциального роста или распада квантовых состояний с течением времени.
В физике число e появляется в задачах экспоненциального распада и роста, где оно представляет собой основание натурального логарифма. Он также используется для расчета непрерывно начисляемых процентов, а также времени, необходимого для увеличения количества на определенный коэффициент.
В математике e — это константа, которая появляется во многих математических уравнениях, включая показательную функцию и логарифмические функции. Он также используется в исчислении, где появляется в формуле производной экспоненциальной функции. Кроме того, e используется в тригонометрии для нахождения значений экспоненциальных и логарифмических функций.
Таким образом, e — это универсальная и важная математическая константа, имеющая многочисленные применения в физике, математике, финансах и других областях науки.
Опрос:
В опросе участвовали 20 человек
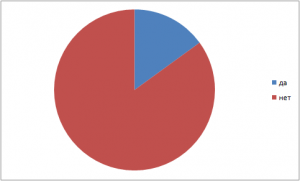
Вы слышали о числе е? 15%-ранее не слышали о числе е
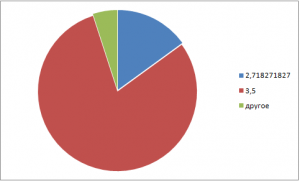
Назовите численное значение числа е.на этот вопрос правильно ответили 80% опрошенных
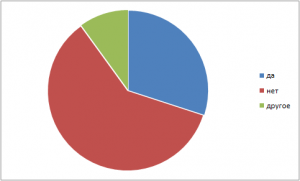
Только ли в математике встречается число е? нет ответили 60%
Вывод:
Удивительно, но число е настолько многогранно, что к нему можно прийти, рассматривая самые разные математические задачи.Число е играет огромную роль в математике и прикладных науках.В банковском деле оно позволяет определять прирост денег при непрерывном начислении процентов.