Автор: Сидельникова А.А. МИФ-МИБz-21
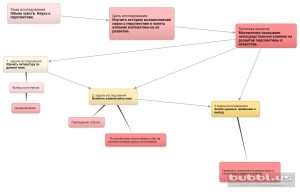
Тема исследования: Обман чувств. Наука о перспективе.
Цель проекта: Изучить историю возникновения науки о перспективе и понять влияние математики на ее развитие.
Задачи проекта:
- Изучить литературу по данной теме.
- Выявить взаимосвязь наук.
-
Анализ данных, сравнение и вывод.
Гипотеза проекта: Математика оказывает непосредственное влияние на развитие перспективы в искусстве.
Методы исследования:
- Выбор и ознакомление с литературными источниками.
- Проведение опроса среди лиц 18-35 лет.
- Анализ данных, сравнение и вывод.
Развитие математики и других естественных наук на протяжении долгого времени шло параллельно. Поэтому научные открытия, сделанные в то или иное время, были зависимы от уровня развития математических дисциплин.
Физика, астрономия, а в последнее время также экономика и статистика, общественные науки и все связанные с информацией дисциплины основаны на математике, используют математические модели или применяют математику в качестве вспомогательного инструмента. Такая закономерность не вызывает сомнения.
Что же касается взаимосвязи творческих дисциплин и математики, то тут связь не всегда очевидна. Однако, математика и творчество как направление человеческой деятельности развивались параллельно. А именно, открытие математической перспективы в эпоху Возрождения ознаменовало переворот в живописи и переход от средневековых концепций к чему-то совершенно новому. В эпоху Возрождения профессии художника, архитектора и математика смешались: многие художники были математиками, многие математики — художниками, и эта взаимосвязь обогатила и математику, и искусство.
Понятия времени, пространства и меры волновали людей начиная с древних времен. Эти понятия рассматривались в философии, равно как и в математике и живописи. В то же время искусству не чуждо математическое мышление. Особая методология математики и восприятие реальности с математической точки зрения способны помочь в изучении произведений искусства, понимании их ценности; в целом они способствуют иному взгляду на результаты творчества художников.
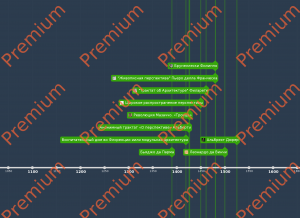
Математика и искусство имеют длительную историю взаимоотношений. Живописцы прибегали к математическим концептам с IV века до н. э. Древнегреческий скульптор Поликлет Старший, предположительно, создал сочинение «Канон» и скульптурный образец (сохранился в приблизительных репликах) идеальной фигуры атлета. Неоднократно высказывались предположения об использовании античными художниками и архитекторами золотого сечения, однако серьёзных подтверждений этому нет. Итальянский математик Лука Пачоли, важная фигура итальянского Возрождения, написал трактат «Божественная пропорция» (лат. De Divina Proportione), иллюстрированный ксилографиями по рисункам Леонардо да Винчи. Другой итальянский живописец Пьеро делла Франческа развил идеи Евклида о перспективе, написав трактат «О перспективе в живописи» (итал. De Prospectiva Pingendi). Гравёр Альбрехт Дюрер в своей знаменитой гравюре «Меланхолия» дал множество скрытых символических отсылок к геометрии и математике. График XX века М. К. Эшер, консультируемый математиком Гарольдом Коксетером, широко применял образы паркета и гиперболической геометрии. Художники движения «Де Стейл» во главе с Тео ван Дусбургом и Питом Мондрианом явным образом использовали геометрические мотивы. Математика оказала влияние на различные формы вязания, вышивки, ткачества и ковроделия. Для исламского искусства характерны симметрии, присутствующие в персидских и марокканских кладках, перфорированных каменных ширмах Великих Моголов, распространённых сотовых сводах.
Именно математика снабдила художников такими инструментами, как линейная перспектива, анализ симметрий и передала им всевозможные геометрические объекты, например, многогранники или ленту Мёбиуса. Преподавательская практика вдохновила Магнуса Веннинджера на создание разноцветных звёздчатых многогранников. В картинах Рене Магритта и гравюрах Эшера используются рекурсии и логические парадоксы. Компьютерным формам искусства доступна фрактальная графика, в частности, визуализация множества Мандельброта. В некоторых работах иллюстрируются клеточные автоматы. Художник Дэвид Хокни высказал горячо оспариваемую гипотезу о применении его коллегами камеры-люциды ещё со времён Возрождения — она помогала точно изобразить место действия. Архитектор Филип Стедмэн утверждает, что Ян Вермеер задействовал камеру-обскуру.
Связь между математикой и искусством выражается и во многом другом. Предметы искусства подвергаются алгоритмическому анализу с помощью рентгенофлуоресцентной спектроскопии. Было установлено, что традиционный батик со всех уголков Явы имеет фрактальную размерность от 1 до 2. Наконец, искусство дало толчок некоторым математическим исследованиям. Филиппо Брунеллески сформулировал теорию перспективы, делая архитектурные чертежи, а позже Жерар Дезарг развил её, заложив основы проективной геометрии. Пифагорейская идея о Боге-геометре созвучна принципам сакральной геометрии, которая также нашла отражение в искусстве. Характерный пример — «Великий архитектор» Уильяма Блейка
Практическая часть исследования
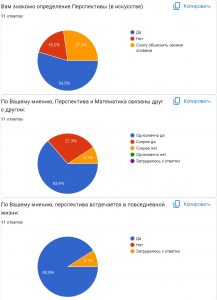
Для того, чтобы узнать на сколько люди владеют информацией о связи математики и перспективы было проведено анкетирование. Результаты анкетирования:
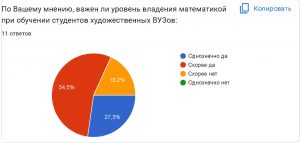
Результаты опроса показали, что большинство молодых людей (18-35лет) имеют представление о перспективе, а также считают что она связана непосредственным образом с математикой. Большая часть считает что перспектива встречается ежедневно в жизни человека. Из числа опрошенных 81,8% считают, что уровень владения математикой важен при обучении студентов художественных ВУЗов и в современное время. Только 18,2% считают иначе.
С практической точки зрения была изучена история влияния наук друг на друга в ходе исторического развития. Результаты исследования предложены в виде презентации.
Список использованной литературы:
1. Буйнов А.Н., Смирнов Г.Б. Первоначальные сведения о перспективе. Москва ВЦСПС Профиздат, 1960г.
2. Касальдеррей Ф.М. Обман чувств. Наука о перспективе. Том 16. Россия, ООО «Де Агостини», 2013г.
3. Федоров С.А., Семенова М.Н. Изобразительное искусство, М: «Просвещение», 1968г.
4. Математика и изобразительное искусство Дата обращения: 18.11.2022г.