Мы всегда считали, что математика — это наука точная, но никогда не задумывались, есть ли в этой науке странные высказывания, расходящиеся с общепринятыми мнениями.
Тизер к исследованию:
https://www.powtoon.com/s/fIjQShv259t/1/m
Цель исследования: выяснить есть ли в математической логике парадоксы.
Гипотеза: в теоретической логике всегда существовали парадоксы.
Задачи:
- Изучить понятия математической логики и парадокс.
- Изучить интересные парадоксы математической логики.
- Провести опрос.
- Проанализировать исторические события.
- Сделать выводы из полученной информации.
Методы исследования:
- Изучение и обобщение
- Анализ и синтез
- Опрос
И для большего показа парадоксов я создала хронологическую ленту, где мы можем увидеть, что парадоксы стали появляться до нашей эры по XX век нашей эры.
Историческая хронология событий:
Исследование:
Для полного понимая данной темы, я привела несколько понятий и несколько интересных фактов.
Математическая логика — раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычисляемость и прочие аспекты оснований математики.
Парадокс — странное мнение, высказывание, расходящееся с общепринятыми мнениями, научными положениями, а также мнение, противоречащее здравому смыслу.
Следующим этапом я просмотрела еще несколько статей и по ним создала презентацию: https://prezi.com/p/kbktfs6o7upv/?present=1
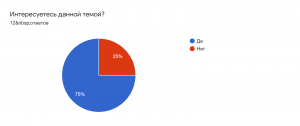
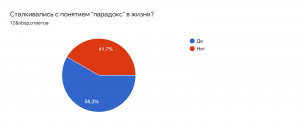
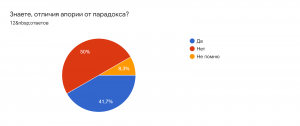
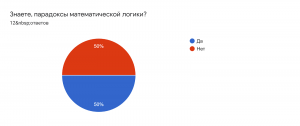
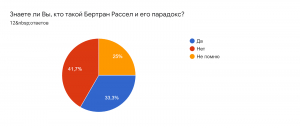
Последним этапом моего исследования был опрос. Вот что получилось в результате:
Интересные парадоксы:
- Из школьных уроков математики всем известно, что такое натуральные числа: это 1, 2, 3, 4, 5… и так далее до бесконечности. Только само понятие бесконечности приводит к парадоксальным свойствам этих чисел. Среди натуральных чисел, как известно, есть чётные. Может сложиться впечатление, что натуральных чисел больше, чем чётных. Вроде бы логично, ведь чётные числа — это только часть натуральных чисел. Но математика утверждает, что чётных чисел столько же, сколько натуральных! Представь себе две строки чисел, в одной — все натуральные числа, а во второй — чётные, то есть числа, полученные умножением на два каждого числа первой строки (1×2 = 2, 2×2 = 4, 3×2 = 6, 4×2 = 8, 5×2 = 10…):
И если эти две строки с числами продолжать до бесконечности, то под каждым натуральным числом будет стоять чётное число. Выходит, что чётных чисел не меньше, чем натуральных. На это удивительное свойство бесконечности обратил внимание в XVII веке знаменитый итальянский учёный Галилео Галилей, который одним из первых и сформулировал этот парадокс.
2. Проблема двух конвертов
Этот парадокс был давно известен математикам, однако в сегодняшнем виде он был сформулирован лишь в 1980-х. Состоит он в следующем:
Двум игрокам выдают по одному конверту. В каждом из них находится некая сумма. Известно лишь, что количество денег в одном конверте вдвое превышает количество в другом. Затем игрокам дается возможность обменяться конвертами.
Что выгоднее: оставить себе полученный конверт или обменяться с оппонентом? На первый взгляд оба варианта равновероятны.
3. Кроме логических, есть ещё парадоксы самоотносимости.
Главный герой такого парадокса пытается применить его условия по отношению к самому себе. Вот какой парадокс придумал знаменитый британский философ и математик Бертран Рассел в начале ХХ века, и вовсе не для развлечения, а когда занимался одной из математических теорий.
В одной деревне был один-единственный парикмахер-брадобрей. Для работы ему было установлено твёрдое правило: он должен брить только тех жителей деревни, которые не бреются сами. Казалось бы, нормальное правило. Вот только у самого брадобрея тоже растёт борода, и встал вопрос: может ли он сам себя побрить?
Получается, что может и… не может. Посуди сам: если он себя не бреет, значит, согласно правилу, он себя брить может. Но если он будет бриться сам, то опять же по правилу он не имеет права себя брить. И хотя Рассел сформулировал этот парадокс строго математически, брадобрею от этого не легче: придётся ему ехать бриться в другую деревню.
4. Парадокс разности квадратов:
а ^ 2-а ^ 2 = а ^ 2-а ^ 2 — имеем равенство
а (а-а) = (а + а) (а-а) — в первой части вынесено общее множитель за скобки, во втором воспользуемся формулой
а = а + а — сократим на общий множитель
а = 2а
5. Лампа Томсона (1954г.)
Представьте себе настольную лампу с кнопкой выключения питания. Допустим, мы включаем лампу на минуту, затем выключаем на 30 секунд, затем вновь включаем на 15 секунд и т. д., с каждым разом уменьшая вдвое время включения и выключения лампы. Возникает вопрос, будет ли лампа включена или выключена по истечении 2 минут?
Ответ на этот парадокс дать невозможно, поскольку следуя в точности логике эксперимента, мы должны бесконечно включать и выключать лампу, так и не достигнув назначенного времени.
Выводы:
Обратная связь по результатом выступления:
https://forms.gle/cEwg7do7AwqbbCnz6
Источники:
- math.wikireading.ru (дата обращения 13.07.2020)
- https://naked-science.ru/ (дата обращения 13.07.2020)
- https://ru.wikipedia.org/wiki/ (дата обращения 10.07.2020)
