Тема исследования: Математическая логика в повседневной жизни человека.
Проблема исследования: Нужна ли математическая логика в повседневной жизни человека?
Цель исследования: Выяснить роль математической логики в повседневной жизни человека.
Гипотеза исследования: Применение математической логики в повседневной жизни человека очень важно.
Задачи исследования:
- Сформировать представление о математической логике и математическом мышлении;
- Проанализировать эксперимент, направленный на выявление природы математического мышления;
- Ознакомиться с исторической хронологией событий , проследить за ходом развития математической логики;
- Ознакомиться с интерактивной книгой;
- Узнать мнение опрашиваемой группы относительно данной проблемы;
- Привести примеры применения математической логики в повседневной жизни.
Методы исследования:
- Изучение и обобщение полученной информации относительно математической логики;
- Изучение развития данного понятия и поставленной проблемы;
- Анализ информации по данной проблеме;
- Опрос с целью выявления мнения по данной проблеме;
- Эксперимент связанный с данной проблемой.
Ход исследования:
Изучив различные статьи в сети Интернет и некоторую литературу, можно дать определение понятиям математическая логика и математическое мышление.
Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем, которые также лежат в основе работы любого компьютера.
Математическое мышление – это абстрактное теоретическое мышление, объекты которого лишены вещественности, но при этом они могут быть интерпретированы любым произвольным образом с одним лишь условием – должны сохраняться заданные между объектами отношения.
Принципиальное отличие математической логики от житейской — это навык «копать глубже», критичность восприятия информации — не принимать слепо на веру любые утверждения, устоявшиеся шаблоны, стремиться искать смыслы, причины, выяснять суть явлений и понятий.
Человек с развитой математической логикой:
- уверен, что любая проблема имеет решение;
- способен разложить поиск решения на последовательные этапы — задачи и подзадачи;
- готов воспринимать ошибки не как препятствия и поражение, а как ступеньки на пути к правильному решению.
Эксперимент:
Ученые уже не один десяток лет пытаются понять, откуда вообще в человеке есть способность к проведению математических вычислений. Для объяснения этого феномена предложены две теории. Смысл первой сводится к тому, что склонность к математике – это побочный эффект появления речи и языка. А вторая говорит, что причиной всему возможность применения интуитивного понимания пространства и времени, причем корни этого понимания тянутся вглубь веков.
Пытаясь понять, какая же теория верна, психологи провели эксперимент, для которого взяли 15 обычных людей и 15 математиков с одним и тем же уровнем образования. Обеим группам предлагали несколько сложных математических и не математических утверждений, и участники должны были оценить их истинность, ложность или бессмысленность. Во время эксперимента мозг каждого испытуемого сканировался томографом.
В результате выяснилось, что заявления, касавшиеся математических областей (геометрии, алгебры, топологии, анализа и т.д.), возбуждали участки префронтальной, нижневисочной и теменной коры головного мозга только у математиков, но не у второй группы испытуемых. И эти зоны отличались от тех, что активизировались у каждого испытуемого при обработке нематематических утверждений. Вышеназванные зоны «работали» у обычных людей только тогда, когда они решали простейшие арифметические задачи.
С научной точки зрения этот результат объясняется тем, что математическое мышление более высоких уровней задействует нейронную сеть, отвечающую за восприятие времени, пространства и чисел. И эта нейронная сеть отличается от той, что связана с языком. Это приводит нас к выводу, что на развитие математической логики непосредственно влияет развитие пространственного мышления.
Историческая хронология событий
Интересные факты:
- Математики подсчитали, что есть 177147 способов завязать галстук.
- Ошибка опоздавшего американского студента, когда он второпях неверно записал задание на дом, завершилась решением парочки «невыполнимых» задач, над которыми не один год бились светила математики. Кстати, процесс решения занял всего пару дней. Это был Джордж Данциг.
- В 1900 году все результаты математических исследований в мире можно было уместить в 80 книгах. Сейчас же все данные с трудом уместятся в 100,000 книгах.
- Задействовав математическое мышление обычный пирог можно легко разделить тремя касаниями ножа на целых восемь частей, при этом они будут абсолютно равными.
- Парадокс дней рождения гласит, что в группе всего из 23 человек есть 50% шанс, что, по крайней мере, у двух людей совпадут даты дня рождения.
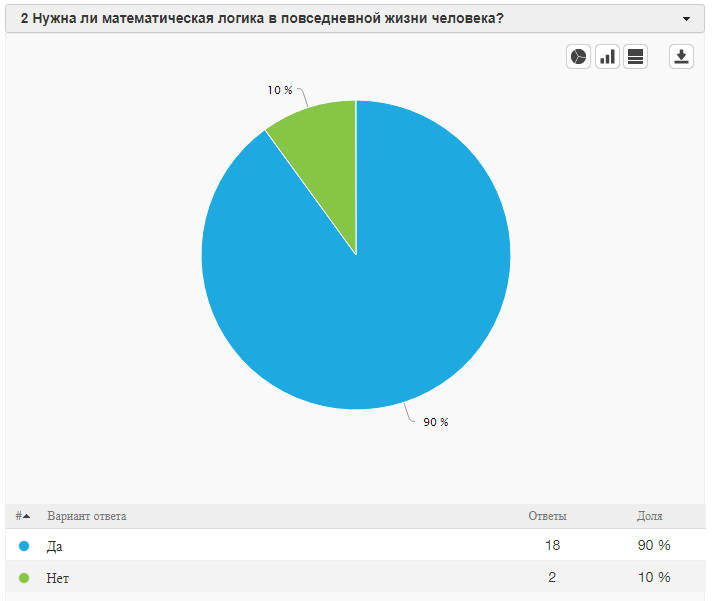
Опрос:
Результаты опроса показали, что большинство опрошенных знакомы с понятием математической логики и применяют ее в повседневной жизни.
Вывод:
Подводя итоги исследования, можно с точностью сказать, что мы достигли реализации поставленной цели и доказали выдвинутую гипотезу. Применение математической логики в повседневной жизни человека очень важно. Она помогает облегчить ему свою деятельность, мыслить точно и последовательно, не допускать противоречий в своих рассуждениях, уметь вскрывать логические ошибки. С помощью нее человек может манипулировать любой воображаемой или реальной пространственной структурой, оценивать ее пространственные отношения и свойства.
Обратная связь по результатам выступления(34 20 60):
Ссылки на разработки проекта:
Ссылки на используемые сервисы интернета: