Число е и его тайны

Число е и его тайны

Тема исследования: Число е и его тайны

Цель исследования: исследовать историю числа е и расширить знания об этом иррациональном числе

Гипотеза исследования: Число е тайно присутствует в нашей жизни

Задачи исследования:

  1. изучить литературу с целью получения информации об истории числа е;
  2.  выяснить его приближенное значение;
  3. рассмотреть различные способы определения числа е;
  4. рассмотреть решение задачи практического содержания проявления числа е в реальной жизни.

План исследования:

Методы исследования:

  • изучение
  • анализ
  • опрос

Этап 1

История

e — основание натурального логарифма, математическая константа, иррациональное и трансцендентное число. Приблизительно равно 2,71828. Иногда число e  называют числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».

Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x  был равен {\displaystyle 10^{7}\cdot \,\log _{1/e}\left({\frac {x}{10^{7}}}\right)}.

Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует.

Предполагается, что автором таблицы был английский математик Отред.

Саму же константу впервые вычислил швейцарский математик Якоб Бернулли в ходе решения задачи о предельной величине процентного дохода. Он обнаружил, что если исходная сумма $1 { и начисляется 100 % годовых один раз в конце года, то итоговая сумма будет $2  Но если те же самые проценты начислять два раза в год, то $1 умножается на 1 , 5 дважды, получая $1 , 00 ⋅ 1 , 5 2 = $ 2 , 25. Начисления процентов раз в квартал приводит к $ 1 , 00 ⋅ 1 , 25 4 = $ 2,441 40625 , и так далее. Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента имеет предел: \lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}. и этот предел равен числу e   ( ≈ 2,718 28 )

{\displaystyle \$1{,}00\cdot \left(1+{\frac {1}{12}}\right)^{12}=\$2{,}613035...}

{\displaystyle \$1{,}00\cdot \left(1+{\frac {1}{365}}\right)^{365}=\$2{,}714567...}

Таким образом, константа e означает максимально возможную годовую прибыль при 100 % годовых и максимальной частоте капитализации процентов.

Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.

Букву e  начал использовать Эйлер в 1727 году, впервые она встречается в письме Эйлера немецкому математику Гольдбаху от 25 ноября 1731 года, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически», 1736 год. Соответственно, e  обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e  применялась чаще и в наши дни является стандартным обозначением.

В языках программирования символу e  в экспоненциальной записи чисел соответствует число 10, а не Эйлерово число. Это связано с историей создания и использования языка FORTRAN для математических вычислений.

Этап 2

Применение числа е

Имея огромное применения в математике, остается неотмеченным вопрос: как же его используют в реальной жизни, то есть каково практическое применение числа Эйлера. Ответ на него столь же прост, как и на вопрос о математическом его применении. Главным образом оно проявляет себя при росте какой — либо величины, будь то рост клетки или банковского счета.

Предположим, что кто-то положил один рубль в банк, выплачивающий 4% годовых. Если проценты простые, то каждый год сумма вклада возрастает на 4% от первоначального капитала. Каждый рубль через двадцать пять лет «вырастет» и превратится в два рубля. Если же банк выплачивает сложный процент, то рубль будет расти быстрее, потому что после каждого начисления процентов капитал немного увеличивается и в следующий раз процент начисляется от большей суммы. Чем чаще производят перерасчет и прибавление прибыли к основному капиталу, тем быстрее растет вклад. При ежегодном начислении сложных процентов рубль за 25 лет превратится

то есть в 2,66 рубля. При начислении сложных процентов каждые полгода (если банк выплачивает 4 (сложных) процента годовых, то прирост вклада за каждые шесть месяцев составляет 2 процента) рубль за 25 лет превратится в

или 2,69 рубля.
В рекламных проспектах банков их составители особо подчеркивают, сколько раз в год производится начисление прибыли. Непосвященному может показаться, что при достаточно частом начислении процентов (например, если производить пересчет миллион раз в год) за 25 лет рубль превратится в весьма ощутимую сумму. В действительности ничего подобного не произойдет. Через 25 лет один рубль вырос бы до величины

где n — число начислений прибыли. При n , стремящемся к бесконечности, это выражение стремится к пределу, равному 2,718 (e), что всего на 3 цента больше той суммы, которая получилась бы, если бы прибыль начислялась лишь раз в полгода. Этот предел и является числом е.

Предположим, что в банке, выплачивающем простой процент, один рубль через какой-то промежуток времени удваивается. При непрерывном начислении прибыли рубль за то же время превратился бы в е рублей независимо от того, сколько простых процентов прибыли выплачивает в действительности банк. Однако за очень большой промежуток времени даже очень маленькая ежегодная прибыль может увеличить первоначальный капитал до гигантской суммы. Если бы в первом году нашей эры кто-то положил один рубль в банк, выплачивающий 4% годовых, то к 1970 году на его счету было бы уже (1,04)1970 рублей, то есть сумма вклада выражалась бы примерно тридцатипятизначным числом.

Однако не все величины возрастают так, как растет капитал в рассмотренных выше примерах. Тип роста, о котором шла речь, обладает одной весьма важной особенностью: в каждый момент времени скорость роста пропорциональна величине того, что возрастает. Иначе, говоря, отношение приращения изменяющейся величины к ее текущему значению всегда одно и то же. Величины такого типа изменяются подобно снежному кому, несущемуся с вершины горы: чем больше становится ком, тем быстрее налипает на него снег. Этот тип роста свойствен многим процессам в живой и неживой природе. Все они описываются формулами, в которые входит экспоненциальная функция. И хотя при расчетах в строительном конструировании инженеры чаще пользуются десятичными логарифмами, в математическом анализе встречаются почти исключительно натуральные логарифмы с основанием, равным числу е.

Если держать гибкую цепь за оба конца, то она провиснет по кривой, которая так и называется — цепная линия (приложение 4). В уравнение этой кривой, записанное в декартовых координатах, также входит число е и уравнение этой кривой имеет вид

Тем же уравнением описывается сечение паруса, надутого ветром: если вертикальная составляющая скорости ветра равна нулю, то он выгибает парус так же, как направленная по вертикали сила земного тяготения изгибает цепь. Маршалловы и Каролинские острова, а также острова Гилберта — это вершины потухших подводных вулканов, в сечении вертикальной плоскостью они имеют форму цепной линии. Цепная линия не принадлежит к числу кривых, называемых коническими сечениями (эллипс, гиперболу и параболу называют коническими сечениями, так как их можно получить на поверхности конуса в пересечении с плоскостью Р, не проходящей через вершину конуса; при этом поверхность конуса мыслится неограниченно продолженной в обе стороны от вершины) (приложение 5), хотя по виду очень напоминает параболу.

Французский энтомолог Жан Анри Фарб в книге «Жизнь паука» дает описание цепной линии, непревзойденное по своему красноречию: «Бессмысленное число е вновь предстает перед нами, начертанное на этот раз на паутине. Выйдя из дому в туманное утро, рассмотрим внимательно сплетенную за ночь паутину. Усеянные крохотными капельками, ее липкие нити провисают под тяжестью груза, образуя цепные линии, и вся сеть становится похожей на множество ожерелий, как бы повторяющих очертания невидимого колокола. Стоит лишь лучу солнца проникнуть сквозь туман, как паутина начинает переливаться всеми цветами радуги, превращаясь в сверкающую гроздь бриллиантов, и число е предстает перед нами во всем своем великолепии».

Например:

Задача.

Какая непрерывная ставка заменит поквартальное начисление процентов по номинальной ставке 20%?

Решение:

Задача
Пусть темп инфляции составляет 1% в день. Во сколько раз уменьшится первоначальная сумма через полгода?

Решение:

Т.о. инфляция уменьшит первоначальную сумму примерно в 6 раз.

Число е находит применение в интегральном и дифференциальном исчислении, а так же в естественных науках.

Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e–kt, где k – число, характеризующее скорость распада данного вещества. Затухание электрического тока I в простом контуре с последовательным соединением, сопротивлением R и индуктивностью L происходит по закону I = I0e–kt, где k = R/L, I0 – сила тока в момент времени t = 0. Аналогичные формулы описывают релаксацию напряжений в вязкой жидкости и затухание магнитного поля.

Аналогично, если бактерии в питательной среде размножаются со скоростью, пропорциональной их числу в настоящий момент, то по истечении времени t начальное количество бактерий N превращается в Nekt.

Этап 3

Интересные факты

 

  

 

 

Опрос:

В опросе участвовали 20 человек

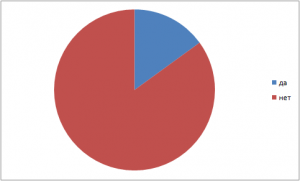
Вы слышали о числе е? 15%-ранее не слышали о числе е

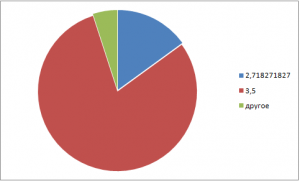
Назовите численное значение числа е.на этот вопрос правильно ответили 80% опрошенных

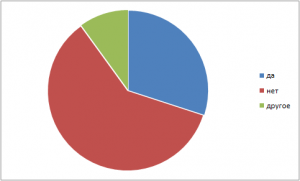
Только ли в математике встречается число е? нет ответили 60%

Вывод по опросу:Участниками опроса стали студенты первого курса.В резудьтате опросы выявлено, что 15%-ранее не слышали о числе е. 35% опрошенных о областях применения числа е

Хронология событий:

https://time.graphics/ru/line/394050

Презентация:

число е

Вывод:

Удивительно, но число е настолько многогранно, что к нему можно прийти, рассматривая самые разные математические задачи.Число е играет огромную роль в математике и прикладных науках.В банковском деле оно позволяет определять прирост денег при непрерывном начислении процентов.

Список литературы:

https://ru.wikipedia.org/wiki/E_(%D1%87%D0%B8%D1%81%D0%BB%D0%BE)   -википедия(история и поределение)

https://урок.рф/library/prezentatciya_chislo_e_i_ego_primenenie_v_finansovih__101604.html  -примеры использования и интересные факты

http://hijos.ru/2010/10/09/chislo-e/  -применение числа е