Волшебное число π

Актуальность: Мы часто, в математических задачах, используем число π, но не знаем в чем же его уникальность. Число π является одним из интереснейших чисел,встречающихся при изучении математики. Оно используется в любых расчетах,где есть окружности. С числом Пи связано много интересных фактов.

Цель исследования: Исследовать число π, его роль в математике и жизни.

Проблема: Что особенного в числе π?

Гипотеза: Есть гипотеза о том, что все (или некоторые) универсальные постоянные со временем меняют свои значения вследствие кривизны пространства или по неизвестным нам причинам.

Поэтому можем предположить, что и рассматриваемое сегодня число π, отражающее свойства Вселенной, может со временем меняться.

Задачи исследования:

1)Изучить историю числа π

2)Найти необычные факты о числе π

3)Выяснить может ли со временем меняться число π

4) Подвести итоги и сделать выводы

Методы исследования:

1)Анализ научной литературы

2)Провести опрос об изученной теме

Этапы исследования:

1)Поиск информации в Интернете и научно-методической литературе о числе π

2)Анализ интересных фактов о числе π

3)Проведение опроса среди однокурсников о числе π

4)Выяснение может ли со временем число π меняться вследствие кривизны пространства

5)Формулировка выводов

В ходе первого этапа исследования мы узнали,что число π(Пи) — математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,141592653589793238462643… Обозначается греческой буквой — π.

Результатом второго этапа является:

Комикс

Этап 3:

Результаты опроса:

1)Знаете ли Вы о существовании числа π ?

(«Да» 20 из 20)

2)Назовите численное значение числа π?

(«3,14…» 20 из 20)

3)Знаете ли Вы о числе π что-нибудь,кроме его численного значения?

60%-Не придавали значения

30%-Нет

10%-Да

4)Для всех ли предметов,имеющих круглую форму,распространяется число π?

67%-да

20%-не задумывался над этим

13%-нет

По результатам анкетирования видно,что тема будет полезна всем.Большинство опрошенных знают числа,помнят матем.формулы,связанные с ним.

Результат 4 этапа:

Опыт №1:

Для начала попытаемся придумать хоть какое-то пространство, где Пи не равно 3.1415… Для этого возьмем метрическое пространство с метрикой, в которой расстояние между двумя точками равно максимуму среди модулей разности координат.

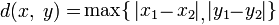
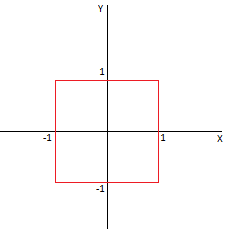
Какой же вид будет иметь единичная окружность в этом пространстве? Возьмем точку с координатами (0,0) за центр этой окружности. Тогда множество точек, расстояние (в смысле заданной метрики) от которых до центра равно 1, есть 4 отрезка, параллельных осям координат, образующих квадрат со стороной 2 и с центром в нуле.

В некоторой метрике это — окружность!

Посчитаем здесь Пи. Радиус равен 1, тогда диаметр, соответственно, равен 2.

Можно также рассмотреть определение диаметра как наибольшего расстояния между двумя точками, но даже так оно равно 2.

Осталось найти длину нашей «окружности» в данной метрике. Это сумма длин всех четырех отрезков, которые в данной метрике имеют длину max(0,2)=2. Значит, длина окружности равна 4*2=8. Ну а тогда Пи здесь равно 8/2=4.

Результат этот практически бесполезен, ведь рассматриваемое пространство абсолютно абстрактно, в нем даже не определены углы и повороты.

Опыт №2:

Попробуем рассмотреть псевдоевклидово (т.к. нас интересуют только двумерные). От обычного евклидового пространства оно отличается тем, что в нем квадрат расстояния между двумя точками может быть отрицательным. Возьмем метрику, в которой скалярное произведение в декартовых координатах будет иметь вид .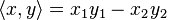

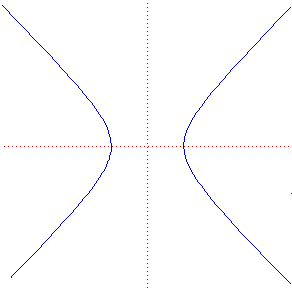
Какой же вид примет окружность единичного радиуса? Это будет множество точек, задаваемых уравнением 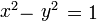, то есть… Гипербола.

В определенном пространстве и это — окружность.

Радиус равен 1, а вот с нахождением длины этой «окружности» есть некоторые сложности. В псевдоевклидовом пространстве такое понятие как «число Пи» вообще не может быть определено, что, безусловно, плохо.

Исходя из всего вышеизложенного,во-первых, попытавшись представить пространство с иным числом Пи,понятно,что оно будет слишком абстрактно, чтобы быть моделью реального мира.

Во-вторых,если попытаться придумать более удачную модель (похожую на наш, реальный мир), выходит, что число Пи останется неизменным. Если принять за данность возможность отрицательного квадрата расстояния (что для обычного человека — просто абсурд), то Пи не будет определено вовсе! Все это и наводит на мысль, что, возможно, мира с другим числом Пи и вовсе быть не могло? Ведь не зря же Вселенная именно такая, какая она есть. А может быть, это и реально, только обычной математики, физики и человеческого воображения для этого недостаточно.

Хронология событий:

Хронологическая лента

Презентация:

Презентация

Вывод:таким образом, на основе проделанной работы можно сказать,что число π для жизни людей играет важную роль. Оно представляет собой не только научную ценность,но и используется для точных вычислений,связано с культурой и природой.