Тема исследования: Математическая модель игры «Мафия».
Цель исследования: Выяснить что такое математическая модель и как она помогает выиграть в игре «Мафия», выяснить роль математики в процессе игры.
Гипотеза исследования: Игра «Мафия» не только психологическая игра, но и математическая.
Задачи исследования:
- изучить и проанализировать информацию, связанную с игрой «Мафия»;
- ознакомиться с психологическими особенностями игры;
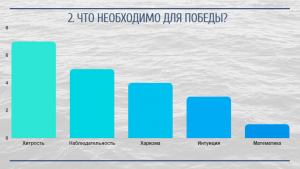
- провести опрос как математика может помочь выиграть в игре «Мафия»;
- выяснить, что такое математическая модель и как она может помочь в игре;
- провести эксперимент с использованием математической модели для победы в игре «Мафия»(контрольная группа без использования математики, экспериментальная группа — с использованием математической модели);
- проанализировать полученную информацию;
- сделать выводы.
Используемые методы исследования:
- Изучение и обобщение полученной информации относительно игры «Мафия»;
- Проведение анализа статей в сети Интернет по данной проблеме;
- Анкетирование с целью получения информации по данной теме;
- Проведение эксперимента позволит подтвердить или опровергнуть выдвинутую гипотезу;
- Анализ и обобщение результатов.
Ход исследования:
История возникновения
«Мафия» — салонная командная психологическая пошаговая ролевая игра с детективным сюжетом, моделирующая борьбу информированных друг о друге членов организованного меньшинства с неорганизованным большинством.
В 1987 году Дмитрий Давыдов, студент факультета психологии Московского Государственного Университета, придумал интересную игру. Сначала в нее играли в общежитиях, в коридорах и аудиториях МГУ. После того, как студенты отдохнули в летних лагерях, игра распространилась по другим учебным заведениям СССР. После окончания университета Д. Давыдов стал преподавателем психологии в МГУ, его лекции посещали студенты из других социалистических стран, они и распространили игру по Европе: в Словакии, Чехии, Венгрии, Польше, Великобритании и других государствах. В США «Мафия» появилась 1989 году (лагерь Пенсильвании).
Правила игры
Рассмотрим правила классической игры. Ведущий раздаёт участникам игры карты рубашкой вверх. Таким образом, формируется команда «мирных жителей»; среди которых есть «комиссар»;, и команда «мафии». Игровой процесс разделён на две фазы: «день»; и «ночь»;. Когда ведущий объявляет в городе фазу ночи, игроки закрывают глаза, «засыпают»;. В первую ночь ведущий позволяет игрокам мафии открыть глаза и запомнить своих соратников, т.е. «познакомиться»;. После чего мафия «засыпает», а ведущий требует проснуться комиссара. Именно так ведущий узнает роли участников. По объявлению фазы дня просыпаются все жители. Днём игроки обсуждают, кто из них может быть причастен к мафии. В конце обсуждения ведущим объявляется открытое голосование за посадку в тюрьму. Самый подозрительный житель, набравший большее число голосов, отправляется за решётку (выходит из игры), а ведущий вскрывает его карту и объявляет игровой статус. Затем наступает фаза ночи. Ночью просыпается мафия, беззвучно (жестами) «совещается» и убивает одного из оставшихся в живых горожан, показывая ведущему кого именно. Мафия засыпает. Просыпается комиссар и указывает на одного из жителей, тем самым проверяя, мафия он или нет. Ведущий всё также беззвучно показывает комиссару статус проверяемого. Днём ведущий объявляет, кто был убит ночью. Этот игрок выходит из игры, его карта показывается всем жителям. Информация о произошедших событиях используется оставшимися в живых игроками для обсуждения и очередного «голосования». Игра продолжается до полной победы одной из команд, когда соперники полностью или посажены, или убиты. Самое оптимальное число игроков: 8-16 человек. При этом формула для расчета количества членов мафии: M = N/k, где M — число мафиози, N — общее число игроков, k — расчётный коэффициент, который обычно варьируется от 3 до 4. Можно брать усредненное значение k = 3,5. Соответственно, количество мирных жителей P = N — M.
Психологические приемы
С точки зрения психологического аспекта, лучшая тактика для игры — быть честным, не зависимо от полученной роли. Тогда игроков можно вычислять по следующим критериям:
- общение (поиск правды и лжи благодаря логическим суждениям);
- эмоции (наблюдение за мимикой, жестами, интонацией голоса и так далее);
- использование схем, которые позволяют определять роль участника не по его действиям и словам, а по действиям и словам других игроков.
Следующие игровые ситуации помогут выработать хорошую тактику.
- Если вы комиссар, то можно сказать об этом, не показывая совей карты. Можно сообщить, кто мафия (если вы угадали ночью ее) или кто мирный (если вы не угадали ночью мафию). Однако мафия также может притвориться комиссаром (прием «лжекомиссарства» тогда вы ставите под угрозу свою жизнь в следующую ночь.
- Если вас убили, то ни в коем случае нельзя сообщать какие-либо сведения об игре. Вы не обладаете правом голоса, однако в спорных ситуациях можно сообщить свои подозрения (в этом случае вы еще не знаете роли других участников).
- Во время игры часто одним и тем же людям достаются мафиозные или мирные карты. Если игрок в своих доводах начинает опираться на теорию вероятности, то скорее всего, он мафия.
- У мафии нет своего мнения, своей позиции. Во время голосования они «присоединяются» к мнению мирных, придерживаются позиции одного из сильных игроков. Они могут намеренно голосовать против своих напарников, подставлять их, чтобы отвести подозрения от команды мафии в целом.
- Для опытного игрока неопытный и честный часто бывает опаснее мафии, поскольку редко поддается убеждению и голосует случайным образом, либо обижаясь, по принципу: «Он проголосовал за меня, вот и я тоже буду против него». Таких также необходимо выводить из игры пораньше, так как их невозможно определить.
- Не зависимо опыта игроков, роль можно определить во время раздачи карт. Начинающие игроки начинают радоваться, опытные стараются вести себя сдержанно. Однако и у последних есть привычки, по которым можно догадаться, кто они: некоторые начинают качаться на стуле, берут что-нибудь со стола и начинают жевать, пьют кофе или чай, почесывают затылок, переглядываются с соседями.
Математический расчет в игре
Математическая модель — математическое представление реальности, один из вариантов модели как системы, исследование которой позволяет получать информацию о некоторой другой системе.
Очень часто мы прибегаем к математическому моделированию в повседневной жизни, не замечая этого. Так же происходит в игре «Мафия».
Во время игры мы стараемся наблюдать за другими, слушать их внимательно, постараться понять, честен ли он по отношению к другим, доверяем ли мы ему. Тем не менее, следует помнить: сколько людей, столько и эмоций, все мы разные. Например, есть игроки, которые будучи мафией, говорят гораздо более убедительные речи, чем когда играют за мирную команду. Если руководствоваться только своим субъективным восприятием речей других игроков, то мафия будет побеждать в 95% игр. Отсюда возникает необходимость понимать математический аспект Мафии и после определенного этапа игры четко следовать ему.
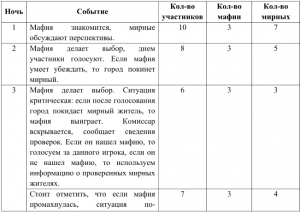
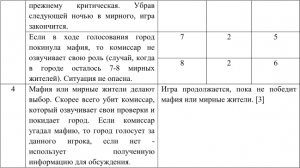
Согласно правилам, мафия выиграла, если количество мирных и мафиозных участников одинаково. Применим математику.
Существуют и более серьезные рассуждения. Рассмотрим ситуацию,
когда осталось 3 игрока: мафия (МФ), маньяк (МН) и мирный житель (МЖ).
Наступает ночь. Кто же выиграет? Ответ на этот вопрос прогнозирует теория
игр . Мирный житель выбирать не может, он просто ждет исхода игры.
Мафия может убить мирного или маньяка, а маньяк — мирного или мафию.
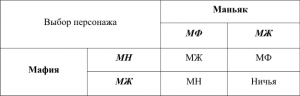
Составим таблицу вариантов, в которой клетки пересечения обозначают
победителя в зависимости от убитых.
Если мафия убивает мирного, то либо выигрывает маньяк, что обидно, либо будет ничья. Если мафия убивает маньяка, то она может выиграть, что является благоприятным результатом игры для мафии, или выигрывает мирный, что из личных побуждений для мафии тоже неплохо. Аналогично рассуждает и
маньяк. Если маньяк убивает мирного, то выигрывает мафия, что плохо для маньяка, либо будет ничья. Если маньяк убивает мафию, то выигрывает либо мирный, либо сам маньяк, в этом случае возможен выигрыш. Получается, что и мафия, и маньяк нацелены убить друг друга, а значит, победа будет за мирным
жителем.
Успешная игра зависит от выбранной стратегии каждого участника. А
если число игроков N, и каждый выбирает свою стратегию S n , то итог игры
находится на множестве S 1 ×S 2 ×…×S n .
Проанализировав вышесказанную информацию из литературы и статей в Интернете, мы можем перейти к следующему этапу: анкетирование среди респондентов 16-26 лет.
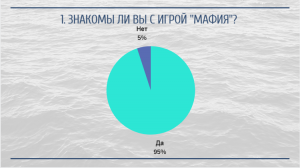
Итог: почти все респонденты знакомы с игрой «Мафия», так как эта игра является одной из самых популярных.
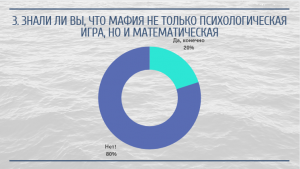
Итог: анализируя данные, полученные в ходе анкетирования, можно сделать вывод, что большинство опрошенных придерживаются мнения, что «Мафия» — это психологическая игра, нежели математическая.
Итог: получаем подтверждение предыдущего вывода, что большинство думает, что «Мафия» — это психологическая игра.
По результатам исследования можно сделать вывод, что большинство опрошенных не догадывались о роли математики в игре.
Было решено организовать эксперимент: случайным образом выбираются 2 группы.
С первой группой была сыграна 1 партия. Так как мы и полагали большинство
участников почти не полагались на математические качества.
Вторую группу мы осведомили о важности математики в игре, показали на примере
как она работает.Затем сыграли партию. Игра была интересней, имела больше логических
доводов и завершилась быстрее, т.к. «мафии» просчитали свои действия на пару «ночей»
вперед, а «мирные жители» проводили дневные голосования очень осторожно и
рассудительно, полагаясь на математический расчет риска возможной ошибки.
Вывод: Таким образом, гипотеза подтвердилась — математика действительно важна в игре «Мафия». Она помогает предвидеть возможные
повороты игры, строить стратегии, оценивать риск на «голосованиях» среди «мирных».
Игроки, которые постоянно прибегают к математике, чаще приводят свою команду к победе.
Используемые источники:
1. Википедия. Математиеская модель (Дата обращения: 02.07.2018)
2. Википедия. Мафия (Дата обращения: 02.07.2018)
3. Факты об игре (Дата обращения: 03.07.2018)
4. Стратегия игры (Дата обращения: 04.07.2018)
5. Правила и разновидности игры (Дата обращения: 05.07.2018)