Проблема.
Как компактнее заполнить плоскость математическими фигурами
Цель.
Узнать какие фигуры компактнее заполняют плоскость
Гипотеза.
Я предполагаю,что компактнее всего заполнить плоскость можно правильными многоугольниками.
Задачи .
1)Выяснить какие фигуры подходят для заполнения плоскости больше всего.
2) Исследовать фигуры самые подходящие для заполнения плоскости.
Методы.
- Изучить научную литературу.
- Провести опрос.
- Найти ответы на поставленные вопросы.
- Подвести итог.
Тизер.
Введение
Термин «мозаика» происходит от латинского mosaicum, что значит «[работа], свя¬
занная с музами». Мозаика представляет собой композицию, созданную из более
мелких частей, которые прилегают друг к другу, составляя единое произведение.
Каждая деталь мозаики называется плиткой, она может иметь строгую геометри¬
ческую форму, хотя это необязательно. Обычно плитки мозаики сделаны из глины,
гранита или стекла, они одинаковой формы и размера, хотя встречаются мозаики,
составленные из плиток разных типов.
Всем нам знакома мозаика: она выложена плитками на полу в наших домах,
кирпичами в стенах, она украшает кафель яркими узорами или представляет собой
одинаковые, равномерно расположенные черепицы на крыше дома.
Хронология событий .
Какие мозаики были во времена Руси и по наш век? Давайте заглянем в историю.
http://www.timetoast.com/timelines/c33b06b4-0fdd-4acc-8f56-fdd53501c767
Изучение.
Способ замощения, при котором используются квадратные плитки, называют
правильным плоским замощением, то есть покрытием плоскости без промежутков
с использованием одного вида правильного многоугольника.
Правильный многоугольник — это выпуклый многоугольник, все стороны
и внутренние углы которого равны. Равносторонний треугольник, квадрат, правиль¬
ные пятиугольник и шестиугольник — это правильные многоугольники с 3, 4, 5 и 6
сторонами, внутренние углы которых равны 60°, 90°, 108° и 120° соответственно.
Когда говорят, что многоугольник выпуклый, это означает, что каждый из его вну¬
тренних углов не больше 180°. У пятиконечной звезды, например, могут быть равны
все стороны и углы, но она является не выпуклым многоугольником, а вогнутым.
По мере увеличения числа сторон форма правильного многоугольника все больше
приближается к кругу — предельной форме правильного многоугольника.
Говорят, что замощение плоскости правильное, если в вершинах сходится всегда одно и то же количество правильных многоугольников одного и того же вида.
Среди огромного разнообразия орнаментов выделяют «паркеты» (мозаики).Паркетом называют заполнение плоскости одинаковыми фигурами, которые не перекрывают дру друга и не оставляют на плоскости пустого пространства (иногда паркетом называют заполнение плоскости несколькими фигурами, например, правильными многоугольниками.
Тетрадный лист в клеточку представляетс собой
простейший паркет. Элемнтом паркета здесь является квадрат.
Элементом паркета является также равносторонний треугольник, правильный шестиугольник, произвольный параллелограмм, даже произвольный четырехугольник.
Правильные многоугольники в природе
Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника?
Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья воск для изготовления ячеек.
Причем пчелиные соты представляют собой не плоский,а пространственный паркет, поскольку заполняют пространство так, что не остается просветов.
Подробнее о заполнение плоскости математическими фигурами.
https://prezi.com/p/s5mf866ve9jt/
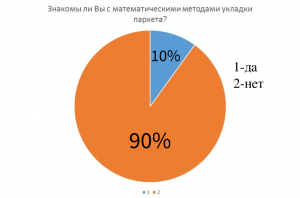
Опрос.
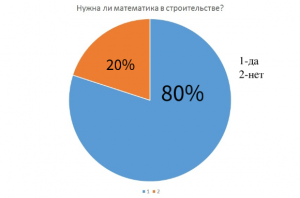
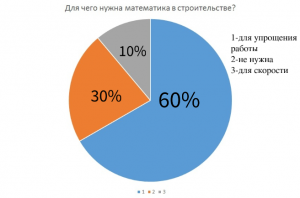
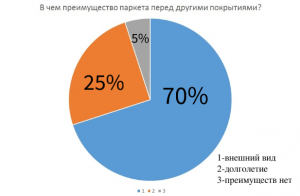
Я провела опрос, знают ли люди для чего нужна математика в строительстве.
Итог опроса.
В результате получаем, что большинство опрошенных знают для чего нужна математика в строительстве.
Интересные комиксы.
Вывод.
Делая вывод из своего исследования, я выяснила , что компактнее всего заполнить плоскость можно правильными многоугольниками.
Опрос