Закономерности в календаре

Цель исследования: Выяснить существуют ли математические закономерности в календаре.

Гипотеза: Предположим, что календарь обладает математическими закономерностями

Задачи:

— Изучить историю календарей и их виды.
— Исследовать задачу про календарь и треугольник.
— Рассмотреть и проанализировать уже существующие закономерности.
— Узнать мнение опрашиваемой группы относительно данной проблемы.
— Выявить новые закономерности.

Методы:

— Изучение и обобщение полученной информации;
— Проанализировать историческую ленту
— Опрос с целью выявления мнения по данной проблеме;

Ход исследования:

Календарь–система счисления длительных промежутков времени, основанная на периодичности таких явлений природы, как смена дня и ночи,смен фаз Луны, смена времени года.
Основными задачами календаря являются:

Фиксация дат;
Измерение интервалов времени;
Определение моментов церковных событий и«дрейфующих» праздников (например, Пасхи).На представленной хронологической ленте можно проследить процесс развития календарей. А также познакомиться с некоторыми их видами.

Историческая хронология событий
Задача «ТРЕУГОЛЬНИКИ В КАЛЕНДАРЕ»
Подробнее разберем задачу:
«Если в календаре 2014 года соединить числа 10, 20 и 30 января, то получится равнобедренный прямоугольный треугольник.»
Решение:

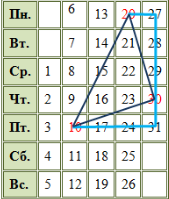Из построения чертежа очевидно, что треугольники с вершинами в числах 30–31–10 и 30–27–20 – прямоугольные, с прямыми углами в вершинах с числами 31 и 27 соответственно. Из чертежа ясно, что стороны 30–31 и 20–27 равны; аналогично равны стороны 31–10 и 27–30.

Отсюда, треугольники 30–31–10 и 20–27–30 равны по двум сторонам и углу между ними. Из

равенства треугольников следует равенство соответствующих их сторон 10–30 и 30–20.

Так как сумма углов в треугольнике равна 180 ̊, получаем, что сумма острых углов в треугольнике с вершинами в числах 31–10–30 равна 90 ̊.

Следовательно, сумма углов, дополняющих угол 30 до развернутого угла, равна сумме острых углов треугольника 31–10–30. Значит, угол 30 тоже равен 90 ̊.

Итак, треугольник с вершинами в числах 10–20–30 является равнобедренным и прямоугольным.

А каков будет результат, если мы соединим числа 10, 20 и 30 любого месяца одного года?Проверим это на табель–календаре 2015 года.

Получим три существенно различных ситуации расположения чисел 10, 20 и 30 в году.

Вывод: Табель–календари обладают следующей особенностью: Если соединить числа 10, 20 и 30 в любом месяце года, то будет получаться равнобедренный прямоугольный треугольник (за исключением тех мест, где центры клеток 10, 20 и 30 лежат на одной прямой).

Видим, что первая ситуация получается, если 1 число месяца приходится на воскресенье, понедельник и вторник.

Вторая ситуация получается, если 1 число месяца приходится на среду, четверг

и пятницу. Если 1 число приходится на субботу, то получаем, что числа 10, 20 и 30 лежат на одной прямой.

Числа 10, 20, 30 отстоят друг от друга на 10 единиц. При их соединении получим равнобедренный прямоугольный треугольник.
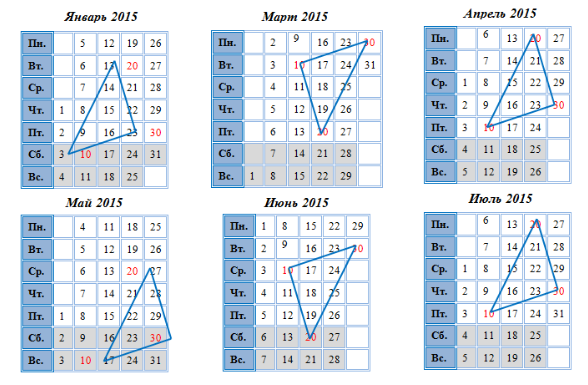
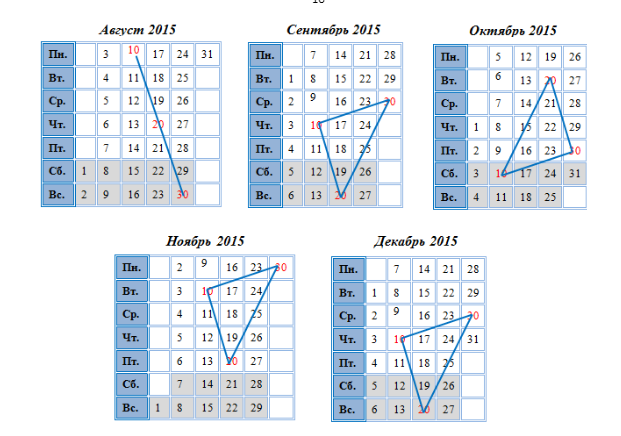
Таким образом, Календари обладают следующей особенностью: если в календаре любого месяца соединить числа, отстоящие друг от друга на 10 единиц, то получится равнобедренный прямоугольный треугольник, за исключением случаев, где центры клеток с числами 10, 20 и 30 лежат на одной прямой.

Занимательные закономерности в календаре

В году будет больше тех дней недели, с которых они начинаются. Так, 2009 год – не високосный, начался и закончился четвергом, значит, четвергов в году будет 53, а остальных дней недели 52.
Любой не високосный год начинается и заканчивается одним и тем же днем недели (2013 год начался со вторника и вторником закончился).
Четные (нечетные) недели месяца повторяются через 2 недели, если первая четная среда 2 числа, то следующие четные приходятся на 16, 28.Чтобы это сделать, вам нужно прибавить к названному числу 8 и результат умножить на 9.
В високосный год на один и тот же день недели в году приходятся:
а) 1 января и 1 октября;
б) 1 февраля, 1 марта и 1 ноября;
в) 1 апреля 1 июля;
г) 1 сентября и 1 декабря.
Високосный год заканчивается со сдвигом на 1 день недели (2012 год начался с воскресенья, а закончился понедельником).
Если в некотором году 1 января – понедельник, а 1 октября – вторник, то год будет високосный.

Таинственные квадраты в календарях

Исследуя календари, мы заметили, что в любом месяце можно выделить квадраты, состоящие из четырех чисел (2×2), из девяти чисел (3×3), из шестнадцати чисел(4×4). Какими свойствами обладают такие квадраты?

Квадрат 2×2
Свойство 1. Сумма чисел на одной диагонали выделенного квадрата, равна сумме чисел на другой диагонали.

Пусть первое выделенное наименьшее число равно n, тогда другие числа будут равны n + 1, n + 7, n + 8.

Сумма первой диагонали равна n + ( n + 8) = 2n + 8.
Сумма второй диагонали ( n + 1) + ( n +7) = 2n + 8. Выражения равны, значит свойство 1 верно.

Свойство 2.Чтобы найти сумму всех четырех чисел достаточно сумму чисел одной диагонали умножить на 2.

Квадрат 3×3

Свойство 3. Чтобы найти сумму девяти чисел в выделенном квадрате календаря,необходимо к меньшему числу прибавить 8 и сумму умножить на 9 или из большего числа вычесть 8 и разность умножить на 9.

Квадрат 4×4
Найдем сумму чисел в таком квадрате. Пусть a-наибольшее число.

a+(a-1)+(a-2)+(a-3)+(a-7)+(a-8)+(a-9)+(a-10)+(a-14)+(a-15)+(a-16)+
(a-17)+(a-21)+(a-22)+(a-23)+(a-24).

Получим, 16a-192=16(a-12).

Значит, сумму чисел в любом квадрате из 16-ти чисел можно находить по правилу:

Из большего числа вычитаем 12 и умножаем на 16 или к меньшему числу прибавить 12
и умножить на 16

Опрос
Заключительным этапом исследования является опрос. В нем принимали участие 21 респондентов в возрасте 17-21 лет.Проанализируем полученные ответы.

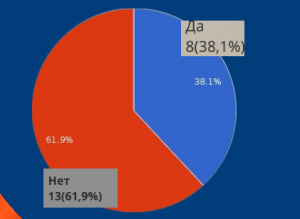
Вопрос №1: Знаешь ли ты, что календарь имеет закономерности?
Вывод: Большая часть опрошенных даже не задумывались раньше о закономерностях в календаре.

Вопрос №2:Сколько закономерностей в календаре ты знаешь?
Вывод: Выяснилось, что некоторую часть опрошенных интересует вопрос закономерностей в календаре.

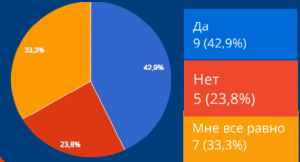
Вопрос №3: Хотел бы ты узнать о закономерностях в календаре?
Вывод:Большая часть опрошенных хотела бы узнать о существующих закономерностях в календаре.

Интересные факты
1)Странный календарь выпустила Волгоградская фабрика офсетной печати. Он имел два февраля, два марта, два июля и два сентября. А вот январь, октябрь, ноябрь в нем и вовсе решили не печатать.

2) В культуре народов африканского государства Гана очень большое значение придают дню недели, в который родился человек — считается, что это оказывает влияние на всю его дальнейшую судьбу. Почти все дети получают первое или второе имя в соответствии с этим днём. Например, у Кофи Анана, бывшего генерального секретаря ООН, имя Кофи означает «пятница». А у популярного футболиста «Челси» Майкла Коджо Эссьена имя Коджо означает «понедельник».

3)Пятница 13-ое не везде считается самым несчастливым днём календаря. В Греции и испаноязычных странах традиционно боятся выпадающего на 13-ое число вторника. А в Италии — пятницы, но 17-го, ведь числа 17 итальянцы опасаются гораздо больше, чем 13. Однако страх перед такими числами может оказывать обратное влияние на вероятность несчастий. Например, центр страховой статистики Нидерландов подсчитал, что в приходящиеся на пятницу 13-ое дни случается меньше аварий и страховых случаев, чем в обычные дни, так как люди склонны вести себя более осторожно или вообще не выходить из дома.

4) У числа Пи есть два неофициальных праздника. Первый — 14 марта, потому что этот день в Америке записывается как 3.14. Второй — 22 июля, которое в европейском формате записывается 22/7, а значение такой дроби является достаточно популярным приближённым значением числа Пи.

5)Самое большое собрание календарей находится в Государственном архиве печати при Книжной палате. Из всех типографий страны сюда на вечное хранение поступают, так называемые, «контрольные экземпляры» не только книг, но и календарей. Здесь собрано около 40 тысяч наименований календарей всех разновидностей.