«Математика и ремонт»

Проблема: «Для чего при проведении ремонта могут потребоваться знания из области математики?»

Цель исследования: Выявить, выполнение каких расчётов будет являться целесообразным при проведении ремонтных работ.

Гипотеза исследования: знания из области математики, при проведении ремонтных работ, необходимы для расчёта требуемого количества строительных материалов, составления наиболее выгодного варианта сметы, а также для поиска максимально приемлемой цены.

Задачи проекта:

1) Провести анкетирование, с целью выявления актуальности поставленной проблемы, проанализировать результаты;

2) Сравнить подходы к измерениям и расчётам в древности и в современном мире;

3) Ознакомить с понятиями «угол», «прямая», «прямоугольник» в жизни;

4) Разобрать суть понятий «периметр» и «площадь» относительно места данных фигур в жизни человека;

5) Показать необходимость математических знаний при расчёте ремонта помещения.

Методы исследования: 

1) Анализ литературы и ресурсов Интернета;

2) Проведение опроса.

«Ничто не нравится, кроме красоты. В красоте – ничто, кроме форм. В формах – ничто, кроме пропорций. В пропорциях – ничто, кроме числа» — Аврелий Августин, философ.

Из истории измерений

С давних пор люди сталкивались с необходимостью определять расстояния, длины предметов, время, площади, объемы и т. д. Измерения нужны были и в строительстве, и в торговле, и в астрономии, фактически в любой сфере жизни. Очень большая точность измерений нужна была при строительстве египетских пирамид. Значение измерений возрастало по мере развития общества и, в частности, по мере развития науки. А чтобы измерять, необходимо было придумать единицы различных физических величин. Вспомним, как написано в учебнике: “Измерить какую-нибудь величину – это значит сравнить ее с однородной величиной, принятой за единицу этой величины”.

Когда древний человек, уже мыслящий, попытался найти для себя пещеру, он вынужден был соразмерить длину, ширину и высоту своего будущего жилища с собственным ростом. А ведь это и есть измерение. Изготовляя простейшие орудия труда, строя дома, добывая пищу, возникает необходимость измерять расстояния, а затем площади, емкости, массу, время. Наш предок располагал только собственным ростом, длиной рук и ног. Если при счете человек пользовался пальцами рук и ног, то при измерении расстояний использовались руки и ноги. Не было народа, который не изобрел бы своих единиц измерения.

Человек хотел знать измерения своего земельного участка, жилища и т.д. Из вышеуказанной потребности возникла наука «геометрия» («гео» — земля, «метрио» — мерить). Измерялись площади земельных участков, емкость сосудов и амбаров, объем вынутой при земельных работах земли. Мы знаем из сохранившихся клинописных записей вавилонян, что единицы измерения площади и объема, были при своем возникновении связаны с материальными потребностями общества. Зарождение геометрических знаний, связанных с измерением площадей, теряется в глубине тысячелетий. Однако имеются вполне достоверные сведения о значительном развитии геометрических знаний в Египте более чем за две тысячи лет до нашей эры. Узкая плодородная полоса земли между пустыней и рекой Нилом ежегодно подвергалась затоплению, и каждый раз разлив смывал границы участков, принадлежавших отдельным лицам. После спада воды требовалось с возможно большей точностью восстановить эти границы, ибо каждый из участков ценился весьма высоко. Это заставило египтян заниматься вопросами измерения, то есть землемерием. Помимо этого, они вели развитую торговлю и поэтому нуждались в умении измерять емкость сосудов. Искусство кораблевождения привело их к астрономическим сведениям. Выдающиеся постройки египтян — пирамиды, которые сохранились до нашего времени, свидетельствуют, что их сооружение требовало знания пространственных форм. Все это указывает на чисто опытное происхождение геометрии.

В древнейшие времена египтяне, приступая к постройке пирамиды, дворца или обыкновенного дома, сначала отмечали направление сторон горизонта (это очень важно, так как освещенность в строении зависит от положения его окон и дверей по отношению к солнцу). Действовали они следующим образом. Для того чтобы найти направление север — юг, втыкали вертикально палку и следили за ее тенью. Она становилась наименьшей, когда ее конец указывал на север. В строительстве очень важно было знать площадь участка, отведенного под застройку. Для этого древние египтяне использовали особый треугольник, у которого были фиксированные длины сторон. Египтяне правильно вычисляли площади некоторых прямолинейных фигур, таких, как прямоугольник, квадрат, треугольник и трапеция.

Около 4 000 лет назад египтяне определяли площадь прямоугольника, теми же приемами, как и мы. То есть, чтобы определить площадь прямоугольника, умножали длину на ширину. Те же египтяне использовали и иные приемы, которые позволяли быстрее измерять площадь земельного участка путем только обхода его по границам, но результат измерения получался с некоторой погрешностью. Единицей измерения площади издревле использовали квадрат.

У вавилонян не было таких геометрических понятий как точка, прямая, линия, плоскость, параллельность. Измерение производилось при помощи веревки. Геометрические познания вавилонян превышали египетские. К задачам, которые вавилоняне решали алгебраическим и арифметическим методом, относятся и многие задания на определение длин, площадей при делении земельных участков, объемов земляных выемок, хозяйственных построек. Все решения, встречающиеся в клинописных текстах, ограничиваются простым перечислением этапов вычисления в виде догматических правил: «делай то — то, делай так — то». В дошедших до нас вавилонских табличках имеются задачи абстрактного характера и внешне кажущиеся не связанными с практическими нуждами. Но это не так: они возникли в результате теоретической обработки условий, первоначально порожденных потребностями практики при межевании земель, возведении стен и насыпей, при строительстве каналов, плотин, оборонительных сооружений и пр. Сохранилось немало планов земельных угодий, разделенных на участки прямоугольной, трапецеидальной или треугольной форм. Но соответствующие геометрические фигуры воспринимались ими как абстрактные, так прямоугольник они называли «то, что имеет длину и ширину», трапецию — «лбом быка», сегмент — «полем полумесяца», параллельные прямые — «двойными прямыми».

Возникает логичный вопрос: «Какими единицами измеряли площадь в древние времена?». Ведь, как было сказано выше, человек столкнулся с необходимостью измерений в глубокой древности, на раннем этапе своего развития – в практической жизни, в земледелии, строительстве своего жилья, дворцов своих властителей, храмов, в торговле. Людям потребовалось измерять расстояния, площади, объемы, веса, и, разумеется, время.

 Единицы измерения в древние времена

Русская система мер — система мер, традиционно применявшихся на Руси и в Российской империи. На смену русской системе пришла метрическая система мер, которая была допущена к применению в России (в необязательном порядке) по закону от 4 июня 1899 года.

 Как измеряют сейчас. Единицы измерения в настоящий момент времени

По подсчету академика Б. С. Якоби (сторонника превращения метрической системы в международную), от замены прежней системы мер на метрическую преподавание арифметики в школе выиграло третью часть времени, отводившегося на этот предмет. Соответственно значительно упростились расчеты в промышленности и торговле.

 

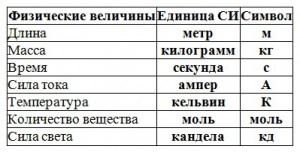
Определения базовых единиц

1. Метр равен расстоянию, которое проходит плоская электромагнитная волна в вакууме за 1/299792458 долю секунды.
2. Килограмм равен массе международного прототипа килограмма.
3. Секунда равна 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия ¹³³Cs.
4. Ампер равен силе постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м друг от друга, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2·10^–7 Н.
5. Кельвин равен 1/273,16 части термодинамической температуры тройной точки воды.
6. Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде ¹²C массой 0,012 кг.
7. Кандела равна силе света в заданном направлении от источника, испускающего монохроматическое излучение частотой 540·10¹² Гц, энергетическая сила света которого в этом направлении составляет 1/683 Вт/ср.

Таким образом, метр, килограмм, секунда, ампер, кельвин, кандела, моль – семь основных единиц системы си.

 Математические знаки

Математические знаки – условные обозначения, которые служат для записи математических понятий, предложений, соотношений. Развитие системы обозначений в математике было тесно связано с общим развитием ее понятий и методов. В процессе становления математических наук возникала необходимость в точных, ясных и сжатых формулировках, требовалось устранить громоздкость словесных описании математических фактов, многозначность в математических выражениях.

Конечно же, ни одно математическое действие в представлении современного человека не осуществимо без столь привычных глазу знаков. Если рассуждать об этом в приложении строительный тематики, то необходимость тех или иных знаков становится очевидной. Так, невозможно узнать площадь комнаты, не воспользовавшись знаком умножения, представить разницу между объёмами двух растворов, не вообразив в голове значки «<» и «>». Точно так же дело обстоит с процентным обозначением и вытекающего оттуда, например, понятия о расчёте скидки на тот или иной материал.

На представленной временной ленте Вы можете наглядно ознакомиться с тем, когда были открыты и приняты обозначения, находящиеся в обиходе современного человечества, а также получить представление о промежутке времени, в который подобные научные изыскания достигли своего пика.

Угол, прямая, прямоугольник, квадрат

Не секрет, что практически любая комната (за исключением, быть может, каких-либо вычурных дизайнерских построек) имеет форму прямоугольника или квадрата, в тех или иных вариациях данных фигур. Также, исходя из жизненного опыта, мы знаем, что каждая комната имеет углы и прямые линии. Посему, можно утверждать, что стык двух прямых, имеющих материальную составляющую и вытянутых в длину, именуемое стенами, образует угол. Четыре стены, соединённые друг с другом в форме привычной человеческому глазу комнаты, будут представлять из себя геометрическую фигуру прямоугольник (квадрат).

В нижеследующем разделе предлагается вспомнить, что же представляют из себя такие понятия как: угол, прямая, прямоугольник, квадрат, а также – какие свойства им присущи.

Понятие и виды углов

Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О, и сторонами k и m.

 

На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.

Развернутый и неразвернутый угол

Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке ниже представлен развернутый угол О.

 

Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла.  На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.

В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).

На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.

 

Измерение углов

Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус. Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.

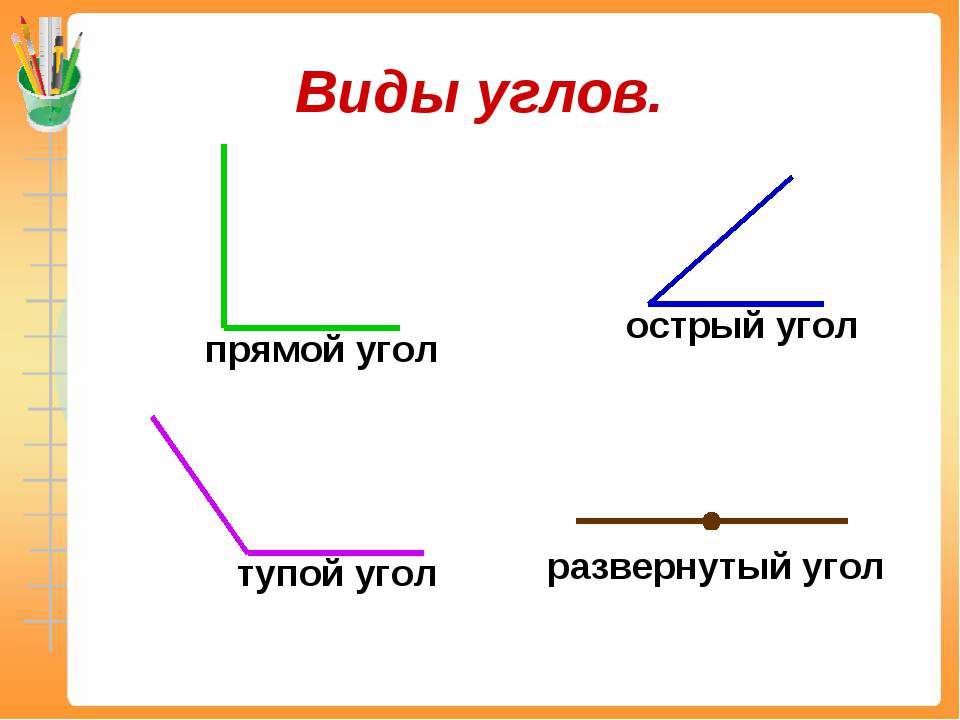
В зависимости от градусной меры углы делятся на несколько групп.

1. Острый угол — градусная мера от 0 до 90 градусов.

2. Прямой угол — градусная мера 90 градусов.

3. Тупой угол — градусная мера больше 90 градусов.

Линия

Прямая линия — одно из фундаментальных понятий геометрии.

Наглядно прямую линию может продемонстрировать туго натянутый шнур, кромка стола, край листа бумаги, место, соединения двух стен комнаты, луч света. При начертании прямых линий на практике применяют линейку.

 Прямой линии присущи такие характерные особенности:

1. У прямой линии нет ни начала ни конца, то есть она бесконечна. Существует возможность начертить только ее часть.

2. Через две произвольные точки можно провести прямую линию, и притом только одну.

3. Через произвольную точку можно провести не ограниченное количество прямых на плоскости.

4. Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны.

Для обозначения прямой линии используют или одну малую букву латинского алфавита, или две большие буквы, написанные в двух различных местах этой прямой.

Если на прямой линии указать точку, то в результате получим два луча:

Лучом называют часть прямой линии, ограниченную с одной стороны. Для обозначения луча применяют или одну малую букву латинского алфавита, или две большие буквы, из которых одна обозначается в начале луча.

Часть прямой, ограниченная с обеих сторон, именуют ее отрезком. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.

Линию, сформированную несколькими отрезками, не лежащими на одной прямой, принято называть ломаной. Когда концы ломаной совпадают, то такая ломаная именуется замкнутой.

 Прямоугольник

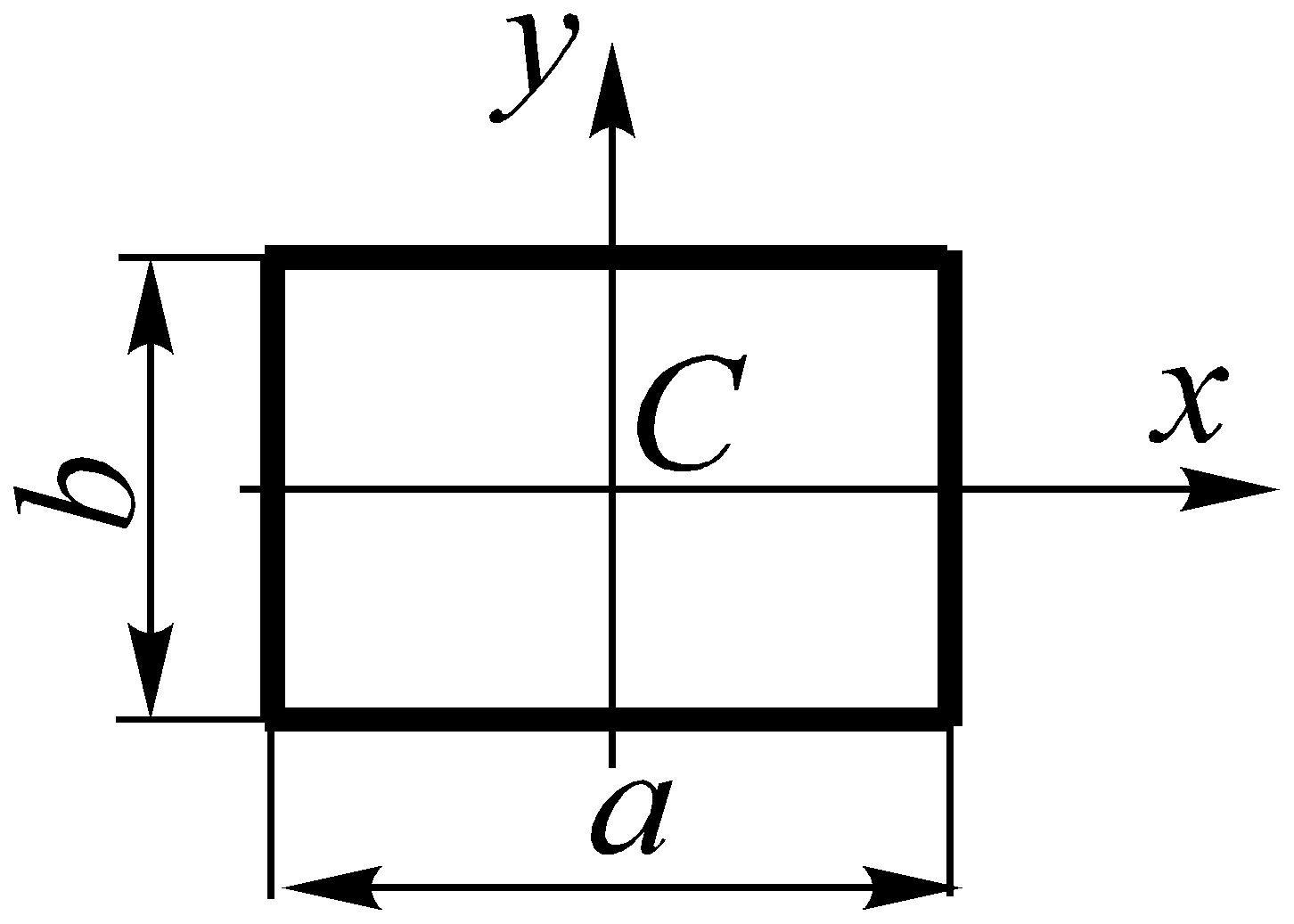
Прямоугольник – это в первую очередь геометрическая плоская фигура. Она состоит из четырех точек, которые соединены между собой двумя парами равных отрезков, перпендикулярно пересекающихся только в этих точках. Если все стороны правильного прямоугольника равны, то такой прямоугольник называют квадратом. Квадрат также определяется как ромб, у которого все его стороны равны между собой, а все углы прямые.

Периметр, площадь

Что такое площадь и периметр?

Площадь – величина, характеризующая размер поверхности, которую занимает геометрическая фигура.

Периметр – размер границ (контура) геометрической фигуры.

Понятия применимы для каждой геометрической фигуры и выражаются в различных единицах. Расчет периметра и площади определяется единицами измерения параметров, используемых для их вычисления: длин сторон, диаметра, высоты. В геометрии указанные параметры чаще всего измеряются в мм, см, м.

Сравнение площади и периметра

В чем же разница между площадью и периметром? Периметр обозначается заглавной буквой P, используется при измерении многоугольников и определяется как сумма длин его сторон. Площадь обозначается буквой S и может быть использована как численная характеристика поверхности, имеющей различный контур, в том числе искривленный. Понятие «квадратура» частично отражает смысл площади, в основе которой положено измерение квадрата поверхности.

Простейший случай – квадрат. Длины его сторон равны, поэтому для вычисления периметра достаточно умножить одну сторону на 4. Формула выглядит так:

Р = a + a + a + a = a х 4, где а – сторона квадрата.

Для вычисления площади квадрата используется другая формула:

S = a х a = a².

Отличие площади от периметра

1. В случае с периметром речь идет о размерах контура, в случае площади – о размерах поверхности.
2. Единица измерения S определяется как квадрат единицы измерения характеристик поверхности, для периметра она равна единице измерения сторон многоугольника.
3. Периметр характеризует размеры многоугольника, площадь – более широкое понятие, применимое для поверхностей с различным контуром.
4. Формулы для определения площадей сильно различаются, а для определения периметра достаточно просто сложить стороны многоугольника.

 Использование математических знаний при выполнении ремонтных работ

Каждый владелец жилого помещения рано или поздно обязательно сталкивается с проблемой ремонта. В связи с этим возникает ряд логичных вопросов: какой выбрать дизайн, сколько закупить необходимого материала, где это можно сделать дешевле и т.д. Но самый важный вопрос: как выполнить работу наиболее качественно? Возможно несколько вариантов:

1) Полностью доверить работу специалистам;

2) Самим произвести расчёт необходимого материала, закупить его, а непосредственное выполнение работы предоставить специалистам;

3) Полностью сделать ремонт самостоятельно.

Чтобы ответить на поставленный выше вопрос, необходимо вооружиться здравым смыслом, математическими расчетами, советами и опытом специалистов. При планировании ремонта нужно профессионально составить смету, чтобы уложиться в бюджет. Строгие правила математики здесь, безусловно, будут крайне необходимы. Стоит отметить, что помимо всего прочего, стройка и ремонт, как и математика, активно развивают мозги, учат находить оптимальное решение в нестандартных задачах (например — как при весьма ограниченном бюджете, осуществить все задуманные идеи).

Для того, чтобы понять, насколько актуальна проблема взаимосвязи математических знаний и проведения ремонтных работ, был проведён опрос общественности.

Исходя из результатов анкетирования, приходим к выводу: большинство людей желает провести ремонт с наименьшими затратами, получив при этом качественный, долгосрочный результат. В связи с этим, предпочтение отдаётся ремонту «своими руками» А это, в свою очередь, означает прямую взаимосвязь необходимости умения выполнять определённые математические расчёты с грамотным планированием и последующим проведением ремонта.

 Интересные факты

Как известно, математика — это мать всех наук. И это немудрено. Поскольку все точные науки сосредоточены на вычислениях. Однако это вовсе не означает, что все в этом царстве скучно и занудно. Отнюдь! Невзирая на всю серьезность учения, появляются удивительные и интересные факты о математике. И найти их можно практически в любом уголке земного шара.

Удивительно, но – факт

Рассмотрим самые интересные факты о математике, касающиеся нашей страны, а также западных государств. Как известно, у нас ноль не принадлежит к множеству натуральных чисел. Но так считают не все: на Западе его относят к натуральным числам. Или вот другой пример.

 

Многие из нас живут и не подозревают, что «сейчас» от них улетает довольно быстро — 86 400 раз за день. Этой единице счисления не дали название, но выяснили, сколько длится миг: примерно сотая доля секунды. Как оказалось, некоторые народы весьма суеверно относятся к тем или иным числам. Например, в Японии и в Китае нет ничего с номером четыре, так как эта цифра олицетворяет саму смерть. Поэтому ее не принято использовать даже в отелях. В Израиле отвергают все, что тем или иным способом связано с христианством, поэтому они не пишут знак «плюс» в математических вычислениях, а обходятся всего-навсего перевернутой буквой «Т». А в азартных играх (рулетка в казино) число 666 — это сумма всех значений, которые присутствуют на барабане.

Занимательные примеры

Каждый человек знает со школьной скамьи, что получится, если сложить все числа от одного до десяти. Вы забыли? Не страшно, напомним: сумма составит 54. Тем людям, которые дружат с точными науками, известно, что если сложить все значения от 1 до 100, то получится весьма внушительное число — 5050. Можно произвести простой расчет и посмотреть, что будет, если ввести в калькулятор первые 3 цифры своего номера телефона (без оператора), умножить их на 80, прибавить 1, далее нужно все это умножить на 250, прибавить последние 4 цифры своего номера два раза, отнять 250, разделить на 2. Ответом будет удивительное число. Оно вас поразит, уверяем!

Шнобелевская премия

Все знают, что такое Нобелевская премия, кому и за что ее вручают. Но помимо нее есть еще одно необычное награждение. Его называют Шнобелевской премией. Кто же может стать лауреатом? Ее вручают одновременно с Нобелевской, но, в отличие от знаменитой премии, Шнобелевскую дают за те гениальные проекты, которые на данный момент не могут воплотить в реальность. Или никогда этого не сделают, потому что они абсурдны. В 2009 году сию награду вручили ветеранам, которые доказали, что корова, имеющая кличку, дает больше молока, чем та, у которой имени нет.

Эксперимент

Удивительно, но ученые провели эксперимент, который показывает, какое расстояние на оси представляют в своем воображении люди, не имеющие образования. В числе испытуемых были представители из племени мундуруку и американские школьники, которые не умеют считать. Им дали посмотреть на определенное количество точек, а после некоторого времени попросили указать, где находятся числа от одного до десяти. Выяснилось, что для большинства людей самые маленькие значения имеют большие расстояния. Как оказалось, в области кулинарии тоже имеют место быть интересные факты о математике. Например, торт можно разрезать двумя способам на восемь ровных кусков.

Полезные советы

Многие люди не знают, как проверить подлинность купюры евро. Но это сделать сравнительно легко. Необходимо взять букву из серийного знака и подставить вместо нее цифру (порядковый номер в алфавите). Затем нужно сложить получившееся число с остальными значениями. А после этого складывать цифры результата до тех пор, пока не выйдет одно значение — 8. Получается, что такие интересные факты о математике могут помочь проверить подлинность купюр. Если взять несколько фигур (среди которых будет круг) с одинаковыми периметрами, то после ряда вычислений окажется, что у круга самая большая площадь. Нельзя не заметить, что если провести расчет периметра круга и остальных фигур, то он останется в меньшинстве. Да, у него самый маленький периметр.

Факты о великих математиках

Альберт Эйнштейн с детства был одарен. Но, имея талант в математике, он не смог поступить в политехническое школьное учреждение Цюриха из-за того, что ему не удалось набрать нужного количества баллов по остальным предметам. Кстати, такие особенности развития отмечены у многих гениев. Вскоре, подтянув знания по нужным дисциплинам, Эйнштейн был допущен к занятиям в этой школе. Существуют и другие интересные факты о известных математиках.

В американском университете аспирант Джордж Данциг смог решить две задачи, которые до этого считали безответными. Дело в том, что будущий математик немного опоздал на урок. После чего с доски он списал эти задачи, решив, что они являются домашним заданием. Они казались сложными, однако у Джорджа за несколько суток получилось закрыть вопрос, над которыми не один год задумывались ученые.

Как оказалось, математике можно научиться не только в школе или в институте, но и дома, рассматривая обои. Во всяком случае это получилось у Софьи Ковалевской. Так вышло, что она в детстве смотрела в своей комнате на листы с лекциями об интегральном и дифференциальном вычислении,. А все дело в том, что на детскую просто не хватило обоев. И слава богу!

Удивительно, но с помощью математики можно узнать, когда наступит последний день пребывания на земле. Абрахаму де Муавру (ученому из Британии) удалось этого добиться через арифметическую прогрессию. Он замечал за собой то, что он начинает каждый день на 15 минут больше спать. Что из этого получилось? Абрахам составил прогрессию, которая указала дату, когда ему предстоит спать 24 часа в сутки. Это оказалось 27 ноября 1754 года. Как раз в тот день математик и скончался.

Занимательные видео

Заключение

Наблюдая различные процессы и явления, мы стараемся разглядеть самые существенные их черты, самые глубокие закономерности. Часто они оказываются общими для широчайшего круга наблюдаемых событий. Общей оказывается и математическая модель, построенная на основе этих закономерностей. И даже проведение ремонтных работ, как было сказано выше, невозможно без элементарных геометрических представлений, а также без простейших вычислительных навыков.

Казалось бы, математика — это лишь цифры, которые необходимы людям для счёта. Но если внимательнее присмотреться, можно увидеть огромное количество случаев, когда она появляется в нашей жизни не только как сложение и вычитание, деление и умножение. Этот факт, подтверждённый приведёнными выше рассуждениями, заставляет посмотреть на математику несколько глубже, чем на науку, никак не связанную с повседневной практической жизнью.

Источники:

• Клименченко Д.  «Величины и их измерение».  —  Н. Ш., № 6, 1990
• Шабалин С.А. «Измерения для всех». —  Издательство стандартов, 1991
• isgeom.narod.ru [Электронный ресурс] URL: http://isgeom.narod.ru/str3.html (дата обращения 03.07.2017)
• festival.1september.ru [Электронный ресурс] URL: http://festival.1september.ru/articles/549850/ (дата обращения 03.07.2017)
• mirznanii.com [Электронный ресурс] URL: http://mirznanii.com/a/313426/vozniknovenie-izmereniy-v-drevnosti (дата обращения 03.07.2017)
• drevoroda.ru [Электронный ресурс] URL: http://drevoroda.ru/interesting/articles/655/2478.html (дата обращения 03.07.2017)
• www.ria-stk.ru [Электронный ресурс] URL: http://www.ria-stk.ru/mi/adetail.php?ID=15277 (дата обращения 03.07.2017)
• www.nado5.ru [Электронный ресурс] URL: http://www.nado5.ru/e-book/ugol (дата обращения 03.07.2017)
• www.calc.ru [Электронный ресурс] URL: https://www.calc.ru/Ponyatiye-Pryamoy-Yee-Svoystva.html (дата обращения 03.07.2017)
• thedifference.ru [Электронный ресурс] URL: http://thedifference.ru/chem-otlichaetsya-ploshhad-ot-perimetra/ (дата обращения 03.07.2017)
• sovetclub.ru [Электронный ресурс] URL: http://sovetclub.ru/chto-takoe-pryamougolnik (дата обращения 03.07.2017)
• imc-peterhof.spb.ru [Электронный ресурс] URL: http://imc-peterhof.spb.ru/metodicheskie-razrabotki/metodicheskie-razrabotki/primenenie-matematiki-pri-remonte-kvartiry (дата обращения 03.07.2017)
• fb.ru [Электронный ресурс] URL: http://fb.ru/article/140383/interesnyie-faktyi-o-matematike-i-matematikah (дата обращения 03.07.2017)
• videouroki.net [Электронный ресурс] URL: https://videouroki.net/razrabotki/proekt-po-matematike-funktsii-vokrug-nas-neobychnoe-v-privychnom.html (дата обращения 03.07.2017)