Можно ли с помощью математики вылечить рак?
Цель исследования:
Выявить взаимосвязь между математикой и проблемой рака.
Задачи исследования:
- Выяснить, были ли в истории попытки связать математику с медициной.
- Исследовать зарождение математики как способ борьбы с раком.
- Узнать были ли случаи победы над раком с помощью математики.
Гипотезы:
- С помощью математики можно узнать причины образования опухолей.
- Использование математических моделей позволяет лучше проанализировать огромные объемы накопленных данных.
- Раковые заболевания можно вылечить с помощью математических моделей.
Этапы исследования:
- Изучить научную литературу.
- Выполнить опрос.
- Найти ответы на интересующие вопросы.
- Подвести итог.
Введение:
Такой болезнью, как рак – не хвастаются. Всем известно об этой страшной патологии. Но еще страшней тот факт, что она стала намного масштабней. За последние пят лет можно проследить определенные тенденции патологии к увеличению. За несколько последних лет число онкологических патологий значительно возросло в бедных африканских странах, в Восточной Азии и России. В рамках нашей страны наибольший процент онкологии фиксируется в регионах с сильно развитой промышленностью, что обуславливается недостаточной экологией.
Зачем нужна математика?
Процесс математизации — внедрения и использования математики и ее методов в исследованиях, осуществляемых естественными и гуманитарными науками, в технике и производстве, начался еще со времен Евклида и Архимеда. Лейбниц выступил с предложениями заменить содержательные рассуждения исчислениями на основе математики, «чтобы с помощью арифметики и алгебры достичь удивительного искусства в открытиях и найти анализ, который в других областях дал бы нечто подобное тому, что алгебра дала в области чисел».
Математика — наука о количественных отношениях и пространственных формах, абстрагируемых от конкретного содержания, разработала и применила на деле конкретные методы отвлечения формы от содержания и сформулировала правила рассмотрения формы как самостоятельного объекта в виде чисел, величин, множеств и математических структур. Именно это позволяет глубже выявлять скрытные логические связи между объектами, от которых абстрагирована форма, вычленять исходные положения, давать точные формулировки и строгие суждения. Математика дает образец дедуктивного мышления и построения теории.
Подробнее о математическом исследовании рака и о математических моделях мы рассмотрим в
Математическое изучение рака: опухоли в компьютере:
Математическое изучение раковых заболеваний проводится с использованием математических моделей и компьютерного моделирования. Математика при этом, во-первых, помогает выдвигать новые гипотезы о причинах образования опухолей, а во-вторых, использование математических моделей позволяет лучше проанализировать огромные объемы накопленных экспериментальных и клинических данных.
Математика и новые пути исследования:
В 2005 году исследователь Антонио Бру из мадридского университета Комплутенсе предположил, что на поздних стадиях раковые заболевания можно излечивать, вызывая сильное и продолжительное воспаление тканей вокруг опухоли. Эта гипотеза стала результатом математических исследований роста раковых клеток. В ходе исследований было отмечено, что рост всех клеток подчиняется одной схеме, которую Бру назвал схемой универсальной динамики роста опухолей. В этой модели клетки на границе опухоли играют определяющую роль в методе лечения, предложенном Бру. Первоначальное скептическое отношение к гипотезе отчасти было вызвано тем, что использованная математическая модель отличалась от классических моделей раковых заболеваний. Во-первых, в ней предполагалось, что рост клеток подчиняется не экспоненциальному, а линейному закону, а во-вторых, считалось, что рост опухоли зависит не от количества питательных веществ, а от свободного пространства. Это прекрасный пример того, как математика подсказывает исследователям новые пути лечения рака
Так же следует отметить ученого Сехё Цой. Он в месте со своими коллегами разработал математическую модель развития раковой опухоли. Учеными были детально проанализированы изображения раковых опухолей и питающих их сосудов. Получившиеся в ходе исследования результаты были подставлены в математические уравнения, описывающие достаточно сложное взаимодействие между раковыми и здоровыми клетками и окружающими их кровеносными сосудами. В конечном итоге появилась математическая модель, которая способна предсказать вероятностные границы роста раковой опухоли на основе распространения кровеносных сосудов вокруг нее. Несмотря на то, что исследования проводились на мышах, полученные результаты оказались очень точными.
Функция Гомпертца:
В 1964 году исследователь по фамилии Лэйрд заметил, что размножение раковых клеток в опухолях определенного типа описывается функцией Гомпертца. Функцию Гомпертца первыми применили страховые компании. Основная ее идея заключается в том, что с увеличением возраста уровень смертности возрастает в геометрической прогрессии. Если мы используем функцию в ином контексте, в частности применительно к раковым заболеваниям Эта функция весьма схожа с сигмоидой (логистической функцией): рост опухоли замедлен в начале и конце процесса. Замедление в конце процесса кажется очевидным, если учесть, что по мере роста опухоли клетки, расположенные внутри нее, получают меньше кислорода, отмирают и вызывают некроз ядра опухоли. В результате ее размер стабилизируется: рост внешней части уравновешивается отмиранием клеток во внутренней части.
Опрос:
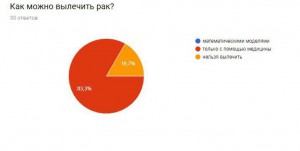
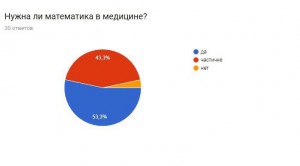
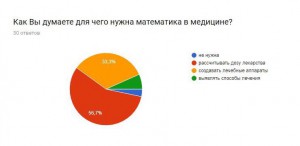
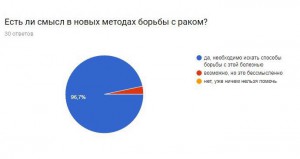
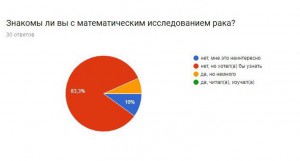
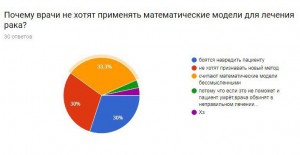
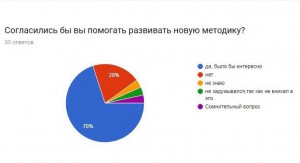
Я провела опрос, чтобы узнать, знают ли люди, что математика очень важна в медицине, не только как способ дозирования лекарства, но и как помощь в исследовании серьезных заболеваний.
Итоги:
В результате получаем, что большинство опрошенных не знают о новых методиках, но им эта тема интересна. Они согласны с тем, что нужно искать новые методы борьбы с раком и необходимо проводить опыты и развивать математику, как лекарство.
Математическое моделирование:
«Математическое моделирование может сыграть важную роль в прогнозировании протекания болезней (в особенности таких, как рак) и составлении индивидуального лечебного плана», — говорят исследователи. — «Индивидуальный лечебный план — это специальный подход к лечению, при котором комплекс медицинских процедур составляется с учетом индивидуальных характеристик пациента: его генетики, физиологии, психологии и др. Пациенты, страдающие от раковых заболеваний, не могут рассчитывать на полноценную медицинскую помощь без индивидуального подхода».
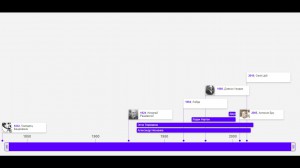
Историческая хронология:
Кто был основателем? Кто проводил математическое исследование рака? Когда зародилась биоматематика? Давайте заглянем в историю развития методики, где найдем ответы на все вопросы.
Опыты и исследования:
По словам экспертов, в ходе осуществления дополнительных наблюдений врачи смогли рассчитать, какой из способов современной терапии является более эффективным для той или иной категории пациентов.В процессе реализации проектов научные работники улучшили результативность оказания медицинской помощи больным, страдающим острым лимфобластным лейкозом. Следует заметить, что анализируя персональные данные и сведения о состоянии здоровья детей, специалисты рассчитали, какой из методов лечения будет самым правильным и эффективным. Во время осуществления исследований авторы проектов установили, почему отдельные препараты или отдельные типы терапий действуют лучше, чем другие. В процессе проведения испытаний у медиков возник вопрос, как результат экспериментов зависит от физиологических свойств пациента.В качестве базы в опытах были задействованы 1773 добровольца. Возраст всех испытуемых составил до 18 лет. Научные работники анализировали влияние пола и диагноза на ход лекарственной терапии. Математическое моделирование позволило найти связь между комбинациями определенных признаков и эффективностью предложенного способа терапии.
Победа над раком:
- Бру и его группе удалось разработать метод лечения, позволяющий полностью уничтожить раковую опухоль, воздействуя на ключевые факторы роста. Новый метод был применен только к одному пациенту, однако достигнутый в ходе лечения «полный успех» позволяет надеяться, что последующие испытания также дадут хороший результат.
- Утверждается, что принявший участие в эксперименте больной страдал от рака печени в терминальной стадии. Исследовав конкретную опухоль, ученые вывели уравнение, решение которого предполагало повышение активности нейтрофилов — разновидности полиморфоядерных лейкоцитов, участвующих в работе иммунной системы человека. Предпринятая в отношении пациента терапия дала немедленный положительный результат без каких бы то ни было побочных эффектов, в результате чего было отмечено полное выздоровление больного и восстановление трудоспособности.
Вывод:
Мы узнали, что не раз была установлена взаимосвязь математики с медициной. Многие ученые обращались за помощью к математики. Испытания комплексной математической модели в реальных клинических условиях показали высокие результаты. Однако, это только первый шаг в создании комплексной модели. Исследователи планируют провести массовые испытания для получения достаточного количества статистических данных, которые позволят значительно повысить точность моделирования, а также расширить область применения модели на все виды онкологических заболеваний. Необходимо развивать новую методику. ведь возможно именно она станет основным лекарством от рака.
Источники:
- Лаос-Бельтра Р. Мир математики №28 «Математика жизни». — де Агостини, 2014
- Математика побеждает рак. [Электронный ресурс] http://www.forbes.ru/tehno/meditsina/47811-matematika-pobezhdaet-rak (дата обращения 04.07.2014)
- Математическое изучение рака. [Электронный ресурс] http://nsportal.ru/ap/library/drugoe/2016/12/13/matematicheskoe-izuchenie-raka (дата обращения 04.07.2014)
- Однако.su [Электронный ресурс] http://odnako.su/news/health/-450479-uchyonye-razrabotali-matematicheskuyu-formulu-dlya-podbora-lecheniya-pri-rake/(дата обращения 04.07.2014)
- Geo. [Электронный ресурс] http://www.geo.ru/nauka/231137-rak (дата обращения 04.07.2017)
- MedikForum. [Электронный ресурс] http://www.medikforum.ru/news/medicine_news/105-matematiki-pomogut-v-lechenii-raka.html (дата обращения 04.07.2014)
- Медицина и математика. [Электронный ресурс] http://nsportal.ru/ap/library/drugoe/2014/10/03/meditsina-i-matematika-referat (дата обращения 04.07.2017)