Шар бесконечного объема. Парадоксы измерения

Тема:  Шар бесконечного объема. Парадоксы измерения

Актуальность: В теореме Банаха — Тарского утверждается, что шар можно рассечь на восемь частей, из которых, в свою очередь, можно собрать два шара, по объему равные исходному.  Ведь если то, о чем говорится в теореме, доказано математически, почему мы не можем, не добавляя дополнительной материи, удвоить шар из золота? Или все-таки мы можем это сделать?

Цели:  Рассмотреть математическое доказательство теоремы и проанализировать, какова ее связь с реальным миром.

Задачи:

• Дать определение понятию «Бесконечность»;
• Рассмотреть парадокс «отель Гильберта»;
• Ознакомиться с доказательством теоремы Банаха-Тарского;
• Дать сравнительный анализ математической теории и физической реальности.

Бесконечность

Для начала следует  определиться с  понятием «Бесконечность» и рассмотреть ее виды.

В математике не существует одного понятия бесконечности, она наделяется особыми свойствами в каждом разделе. Более того, эти различные «бесконечности» не взаимозаменяемы. К примеру, теория множеств подразумевает разные бесконечности, причём одна может быть больше другой. Выделим основные две группы «бесконечностей»:

1. Исчисляемая бесконечность (Кол-во часов в вечности, ряд натуральных чисел и т.д.) Подобные ряды не имеют окончания, однако они исчисляемые. Исчисляемые — означает способность перечислить ряд от начального значения до любого другого за конечный промежуток времени. Даже если этот отрезок времени будет превышать вашу жизнь или время существования вселенной это также — конечный отрезок времени.
2. Неисчислимая бесконечность, или «Континуум» (множество действительных чисел) В буквальном смысле «неисчислимая», поскольку невозможно даже выделить начальное значение.

После рассмотрения диагонального метода Кантора становится очевидным то, что неисчислимая бесконечность значительно больше, чем исчисляемый пусть и бесконечный числовой ряд. Свойства бесконечности подробно объясняет парадокс  «Отель Гильберта».

«Отель Гильберта»

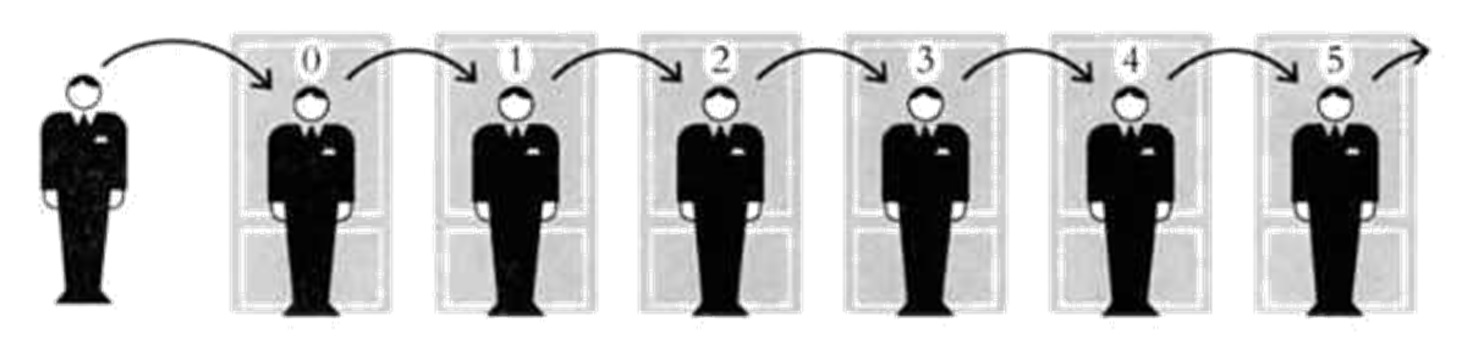
В конце XIX века Давид Гильберт в виде небольшой истории смоделировал математическую ситуацию, которая до сих пор используется для иллюстрации некоторых свойств бесконечности, практически невыводимых интуитивно. Представим, говорит Гильберт, отель, в котором есть бесконечное счетное число номеров, обозначенных цифрами 0, 1, 2, 3, 4, …  

Представим также, что каждый номер занят только одним человеком и что согласно правилам отеля в одном номере ни в коем случае не могут жить два или более постояльцев. В этой ситуации в отель приходит еще один человек, который просит себе номер. Сначала ему отвечают, что это невозможно, поскольку отель полон, однако вновь прибывший предлагает решение: пусть человек, занимающий номер 0, перейдет в номер 1, человек из номера 1 — в номер 2, из номера 2 — в номер 3 и так далее, как показано на рисунке. Так никто не останется без номера, и в то же время номер О освободится для вновь прибывшего.

 

Удивляет в этом примере тот факт, что, вопреки обычной логике и даже здравому смыслу, появление нового постояльца не увеличивает общее количество жильцов, а как до, так и после его прибытия в отеле живет прежнее количество постояльцев.

Любопытно, что предложенное решение было бы справедливым и в том случае, если бы в отель прибыло 10 новых постояльцев вместо одного: для того чтобы все они могли заселиться, не нарушая правил отеля, было бы достаточно, чтобы постоялец из номера 0 перешел в номер 10, постоялец из номера 1 перешел в номер 11 и так далее, так что номера от 0 до 9 окажутся свободными для вновь прибывших.

Более того, общее число постояльцев не увеличивается и в том случае, если добавить бесконечное счетное множество новых гостей. В этом случае постоялец из номера 1 должен перейти в номер 2, из номера 2 — в номер 4, из номера 3 — в номер 6, из номера 4 — в номер 8 и так далее — и все нечетные номера освободятся для размещения новых гостей (см. рисунок).

Так, например, освободится номер 101, поскольку его постоялец переедет в номер 202, постоялец из 202 переедет в 404, а гость из номера 404 — в 808 и так далее. В итоге при добавлении бесконечного счетного количества новых постояльцев общее количество гостей также не меняется, потому что оно соответствует общему числу номеров.

Эти свойства бесконечности позволяют нам проиллюстрировать, как, разрезая тело и перераспределяя полученные части, мы добиваемся кажущегося увеличения материи.

Теорема Банаха — Тарского

Рассмотрим основные шаги доказательства теоремы Банаха — Тарского. Наша цель — доказать, что если дан шар, всегда можно разрезать его на восемь частей, из которых, в свою очередь, можно собрать два шара, равных исходному.

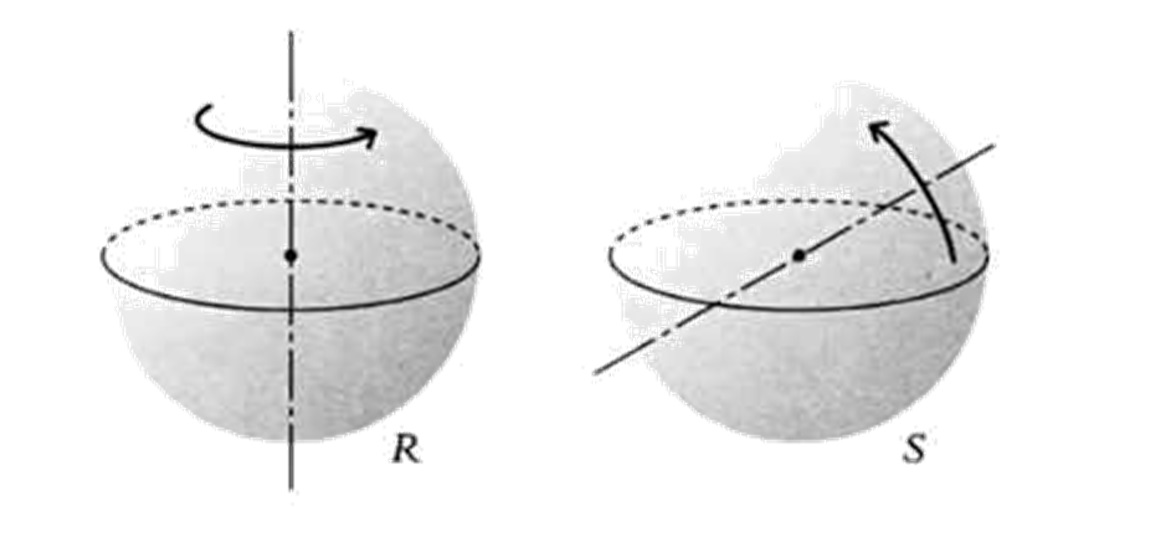
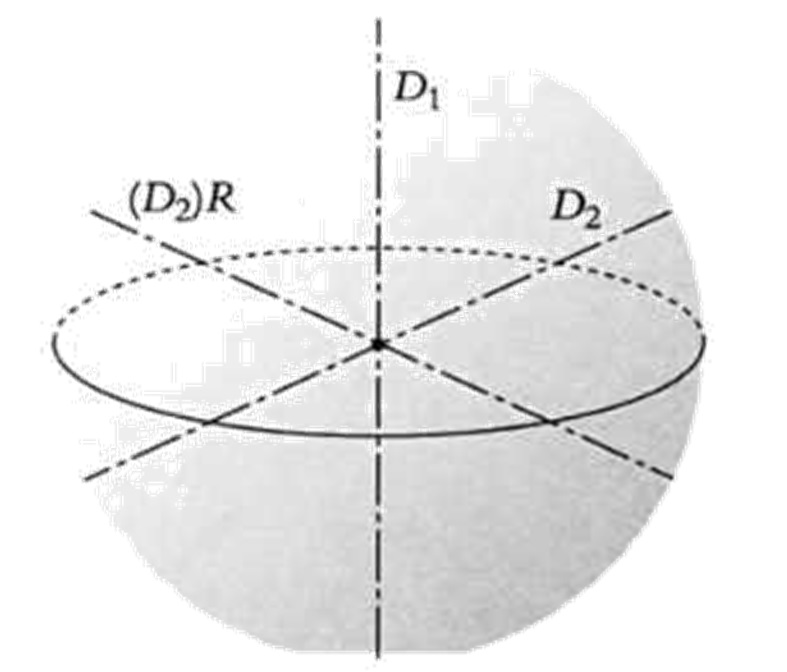
Рассуждение основывается на идее вращения шара вокруг особой оси. Хорошо известно, что каждая точка Земли — как на ее поверхности, так и внутри нее — вертится вокруг воображаемой оси, которая пересекает планету с севера на юг. Любая точка совершает вращение в 360° каждые 24 часа. Очевидно, что если мы возьмем период в 12 часов, то каждая точка сделает оборот на 180°. Это движение, состоящее во вращении всех точек сферы на 180° относительно оси север — юг (фигура слева), обозначим через R, и этот оборот очень важен для наших рассуждений. Следует уточнить, что точки, находящиеся на оси север — юг, неподвижны.

Теперь возьмем вторую ось вращения, которая образует с первой угол в один радиан (около 57°17’45»), и обозначим через 5 движение, состоящее во вращении каждой точки сферы вокруг этой второй оси на угол в 120° (фигура справа на предыдущей странице). Заметим, что если мы осуществим это движение три раза подряд, то каждая точка сферы вернется на свое исходное место. То же произойдет, если мы осуществим два раза подряд вращение R.

Почему для нас важны движения R и S? Как мы уже говорили, при рассечении фигуры (или тела) признак, по которому определяется, что вся совокупность точек является единой частью, состоит в том, что ко всем этим точкам применяются одни и те же движения. Другими словами, точки одной части двигаются сообща и одинаково. В случае рассечения, определенного теоремой Банаха — Тарского, движения, применяемые к частям, на которые делится сфера, это, по сути, комбинации вращений R и S.

Рассмотрим, как комбинируются эти движения. Для этого представим, что сфера снабжена механизмом, который позволяет нам последовательно применять, в любом порядке и сколько угодно раз, вращение R и 5. При этом важен тот факт, что когда мы применяем вращение R, ось, соответствующая обороту 5, не двигается вместе со сферой. Аналогично, когда мы применяем вращение S, не двигается ось вращения R. Таким образом, обе оси все время остаются неподвижными.

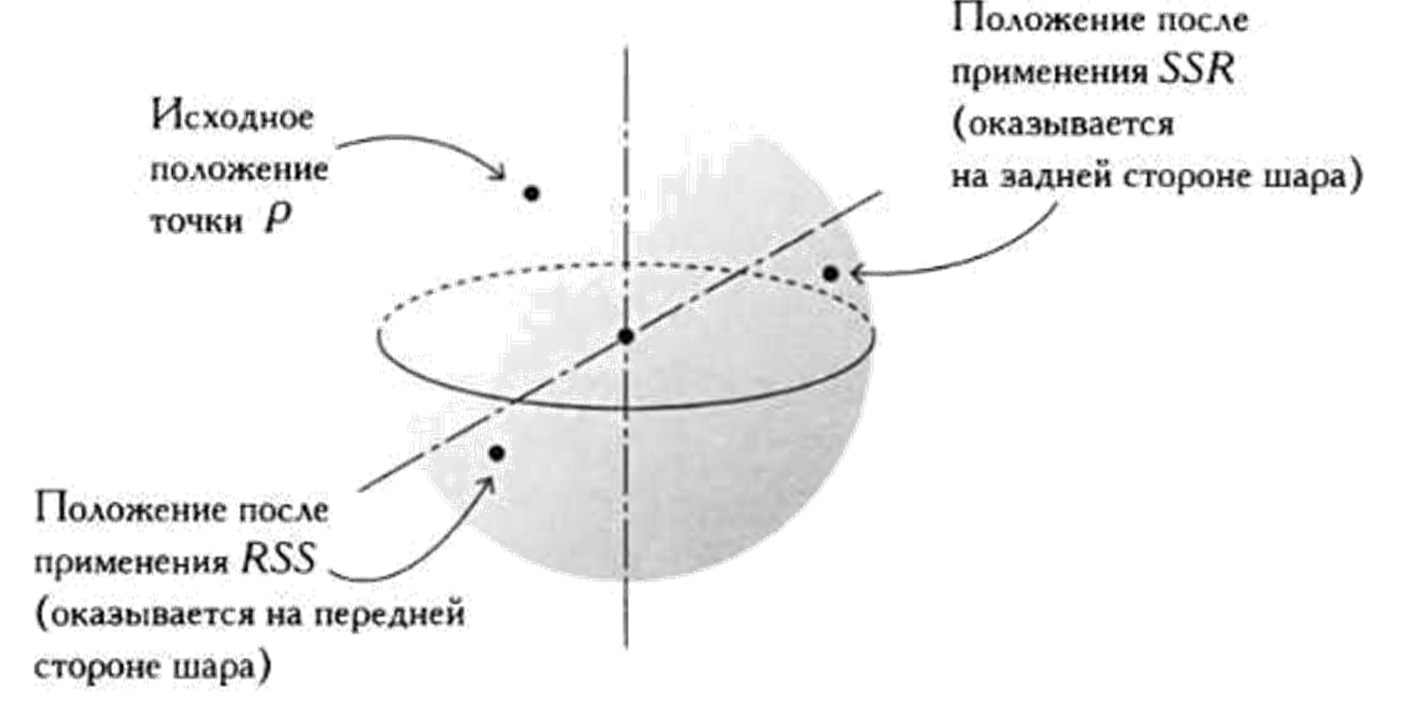
Итак, оба вращения могут осуществляться в любом порядке и любое конечное число раз. Обозначим через RSS движение, которое состоит в том, чтобы сначала применить вращение R, а затем два раза вращение 5; RSSR — движение, состоящее в том, чтобы сначала применить R, затем два раза S и, наконец, снова R, и так далее. Отметим, что движение RSS не то же самое, что SSR, поскольку результаты этих преобразований будут отличаться (см. рисунок)

Итак, каждая комбинация вращений R и 5 описывается с помощью конечной последовательности букв. Отметим, что применить R два раза подряд (так же, как и 5 три раза подряд) — это то же самое, что ничего не делать. Так, RRSSR — это то же самое, что SSR, a RSSSRRRR — то же самое, что R.

С другой стороны, RRSSS равно отсутствию действия; это преобразование мы назовем нулевым движением, и оно состоит ровно в том, чтобы оставить все точки на исходных местах. Кажется странным называть движением действие, при котором ничего не двигается, но в данном случае речь идет об условности, полезной с точки зрения математики. Воспользуемся буквой N для обозначения нулевого движения и в качестве особого случая отметим, что N является сокращенной формой, например, RRSSS (а также RR, SSS, RSSSR и так далее).

Для того чтобы определить части, на которые окажется рассечен шар, мы должны классифицировать все преобразования, полученные в результате комбинации вращений R и 5, на три различные группы. Итак, речь пойдет о движениях 1-го типа, движениях 2-го типа и движениях 3-го типа. Эти три типа движений определяются последовательно, согласно пяти правилам.

Правило 1: R и 5 — движения 1-го типа, N — движение 3-го типа.

Правило 1 классифицирует движения, определенные только одной буквой. В следующих правилах говорится о том, как меняется тип движения по мере того, как к его обозначению добавляются новые буквы. Так, RS состоит в том, чтобы добавить 5 к движению 1-го типа (движение 1-го типа — это, естественно, R)\ то же самое происходит с 55. В правиле 2 говорится, что RS и 55 — движения 2-го типа.

Правило 2: Если движение, записанное в сокращенной форме, состоит в том, чтобы добавить 5 к движению 1-го типа, то это движение 2-го типа (1-й тип + 5 = 2-й тип).

Другой пример — SR, это движение также записано в сокращенной форме и состоит в том, чтобы добавить R к движению 1-го типа. В правиле 3 говорится, что это движение 3-го типа.

Правило 3: Если движение, записанное в сокращенной форме, состоит в том, чтобы добавить R к движению 1-го типа, то это движение 3-го типа (1-й тип + R = 3-й тип).

Чтобы объяснить правило 4, возьмем движения RSR и RSS, которые состоят в том, чтобы добавить, соответственно, R и S к движению RS (которое, как мы уже знаем, относится ко 2-му типу). Правило 4 говорит нам, что RSR и RSS — это движения 3-го типа.

Правило 4: Если движение, записанное в сокращенной форме, состоит в том, чтобы добавить 5 или R к движению 2-го типа, то это движение 3-го типа (2-й тип + 5 или R = 3-й тип).

Наконец, возьмем движение RSSR, также записанное в сокращенной форме, которое состоит в том, чтобы добавить R к движению RSS (3-го типа). В последнем правиле говорится, что RSSR — движение l-ro типа.

Правило 5: Если движение, записанное в сокращенной форме, состоит в том, чтобы добавить 5 или R к движению 3-го типа, то это движение l-ro типа (3-й тип + 5 или R = 1-й тип).

Правила со 2 по 5 заключены в этой схеме.

В формулировке правил (хотя это и опущено в их краткой записи) отмечено, что они применяются исключительно к движениям, записанным в сокращенной форме. И действительно, если бы в правиле 5 говорилось просто, что «при добавлении 5 или R к движению 3-го типа получается движение 1-го типа», то это было бы неправильно, потому что, например, RSR — это движение 3-го типа, но если добавить к нему R, получается RSRR = RS, которое относится не к Ему, а ко 2-му типу. То есть прежде чем анализировать, к какому типу принадлежит движение RSRR, его нужно записать в сокращенной форме.

Можно доказать, хотя мы и не будет делать этого здесь, что эти пять правил позволяют отнести каждое движение, которое получается при комбинации вращений R и 5, к одному из трех типов так, что при этом не возникает неоднозначных толкований.

«Аномальные» точки

Движения R и 5 применяются, как мы уже сказали, ко всем точкам шара — как к лежащим на его поверхности, так и к расположенным внутри. Если Р — это одна из точек, тогда (P)R — результат применения к Р вращения R. Точно так же (P)RSSRS показывает результат применения к Р последовательных вращений RSSRS в таком порядке; заметьте, что (P)N — Р.

Основная идея доказательства теоремы Банаха — Тарского состоит в том, что для каждой точки сферы каждая отличная друг от друга последовательность букв (записанная в сокращенной форме) представляет собой отдельное движение. Это означает, что независимо оттого, какова точка Р, (Р)Р должно отличаться от (P)/V, (P)S, (P)SR, (P)RS, (P)RSR или от результата любой другой последовательности вращений, примененной к Р. При этом (P)R = (P)RSSS, но это не проблема, так как R — это сокращенная форма RSSS.

Однако существует несколько аномальных точек, для которых это условие не выполняется. Например, если Р находится на диаметре сферы, идущем с севера на юг, вокруг которого осуществляется движение R, то это вращение оставляет без движения точку Р, то есть (P)R = Р, и эта точка не удовлетворяет предыдущему условию, поскольку для нее (Р)Р = (P)N и, значит, N и R дают один и тот же результат, если применяются к Р.

Каковы все эти аномальные точки, для которых не выполняется правило: отличная друг от друга последовательность букв (записанных в сокращенной форме) должна всегда давать различные движения?

Обозначим через D] диаметр, вокруг которого осуществляется вращение R, и через D2 — диаметр, вокруг которого осуществляется вращение 5. Мы только что увидели, что точки являются аномальными, и по аналогичной причине таковыми являются и точки D2, но это не все аномальные точки. Предположим, что Р — точка на Dr и назовем Q точку (Р)5, то есть Q получается при применении вращения 5 к точке Р на Dy Тогда получаем, что:

P=(P)R, так как Р — точка на D,;

Q = (Р)5 по определению Q.

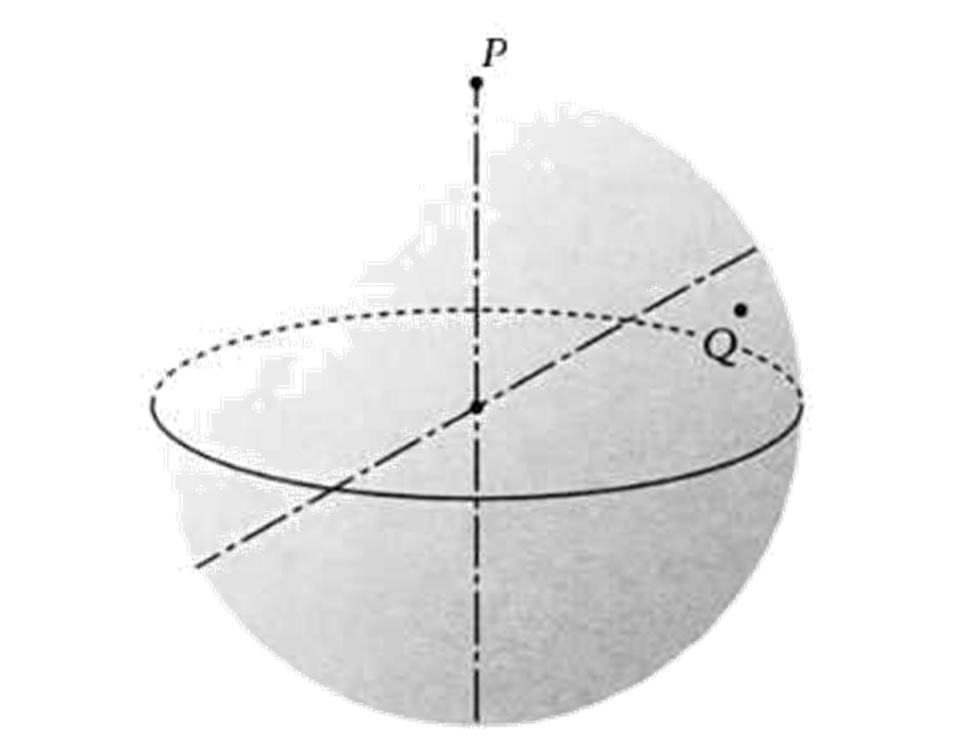
На следующем рисунке показан пример, в котором Р — северный полюс, a Q находится на поверхности сферы, на задней ее стороне, с точки зрения наблюдателя.

Убедимся, что Q также аномальна (хотя она и не лежит ни на одном из диаметров вращения). Для этого докажем, что применение к Q движения SSRS дает тот же результат, что и применение к ней движения /V; то есть докажем, что

(Q)SSRS = (Q)N.

Если в (Q)SSRS заменить Q на (Р)5, увидим, что (Q)SSRS = (P)SSSRS = = (P)RS, так как 555 сокращается, а поскольку (P)R = Р, то (P)RS = (Р)5 и, в свою очередь, (Р)5 = Q, которая равна (Q)/V. Следовательно, (Q)55P5 = = (Q)/V, как мы и утверждали. Значит, Q также аномальна, поскольку существуют отличные друг от друга последовательности, записанные в сокращенной форме (SSRS и N в данном случае), которые, если применить их к Q, дают один и тот же результат.

Таким образом, если ко всем точкам отрезка Dt мы применим вращение 5, то получим целый отрезок, образованный из аномальных точек. Собственно, если к отрезку D, или к отрезку D2 мы применим любую комбинацию вращений R и 5, то всегда будем получать отрезки, образованные полностью из аномальных точек. Можно доказать, что все аномальные точки находятся на этих отрезках, то есть что нет других аномальных точек, кроме тех, что получаются таким образом (тот факт, что нет других аномальных точек, это следствие выбора угла, образованного осями вращения; другие варианты для этого угла, например 20° или 30°, вызвали бы появление дополнительных аномальных точек).

Итак, хотя существует бесконечное число возможных последовательностей букв, эта бесконечность счетная. Таким образом, аномальные точки занимают в целом бесконечное счетное число отрезков (на рисунке показаны три из них). И, как мы отметили ранее, счетное количество отрезков имеет общую площадь, равную нулю, а также общий объем, равный нулю, то есть вся совокупность аномальных точек имеет нулевой объем. Это позволяет нам не учитывать их и сконцентрироваться на остальном шаре. Начиная с этого момента, только если не будет специально от мечено, мы будем иметь в виду точки сферы, которые не являются аномальными.

Продолжение доказательства

Возьмем еще раз движения, обозначенные буквой N и последовательностями букв RhS, записанными в сокращенной форме. Можно доказать, что существует группа точек шара Н, для которых выполнялось бы условие:

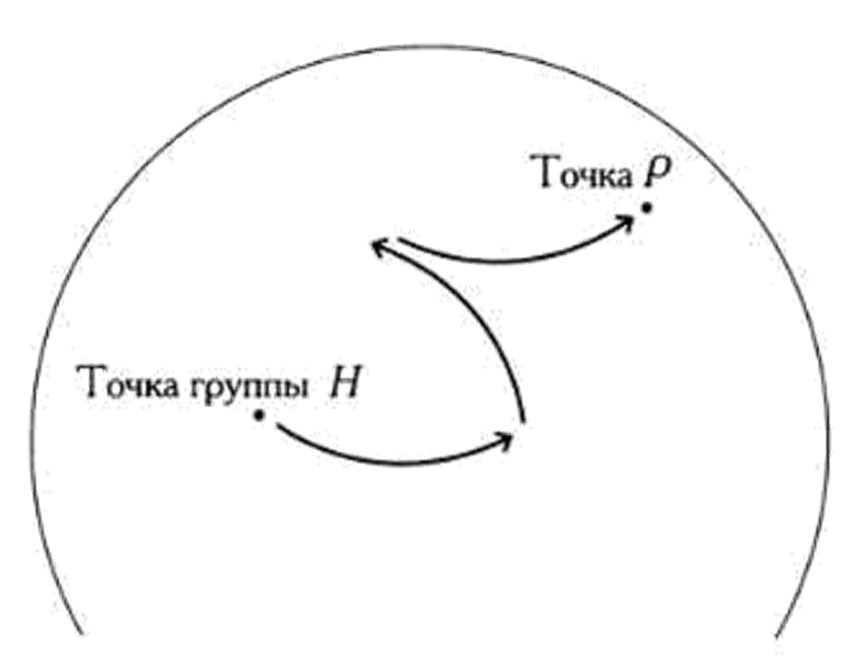
каждой точки шара Р можно достичь, последовательно применяя движения R, 5 и N ровно из одной точки группы Н (см. рисунок).

Другими словами, каждой неаномалыюй точки шара можно достичь из какой-то точки группы Н, выполнив определенную комбинацию вращений RuS. Более того, каждой точки шара нельзя достичь из двух или более точек группы Н.

онечно, этой точки Р можно достичь из других точек Р\ которые не принадлежат группе Н, но эта ситуация для нас неважна. Нас интересуют только движения, которые исходят из точек, принадлежащих Н.

Чтобы понять определение Н, представим себе, что у нас есть только движения R и N, в этом случае нет необходимости говорить о последовательностях движений, поскольку RR = N, RRR = R, RRRR = N и так далее, то есть последовательность букв никогда не дает нового движения. Если бы у нас были только R и N, то было бы относительно просто видно, что из себя представляет группа Н.

Представим еще раз, что шар — это Земля, и мы режем ее, словно апельсин, пополам по Гринвичскому меридиану и меридиану в 180°. Земля окажется разделенной на две полусферы, которые мы можем назвать западным и восточным полушариями. Группа Н может быть образована из всех точек западного полушария, поскольку каждой точки восточного полушария можно достичь, применив вращение R из одной точки западного (заметьте, что это не единственный выбор: мы также можем принять за Н все точки восточного полушария, а также мы могли бы разрезать Землю вдоль любого другого меридиана).

Когда речь идет о движениях R и 5, не говоря уже обо всех их комбинациях, ситуация концептуально похожа на уже описанную, но в этом случае сложность движения настолько велика, что хотя и можно доказать, что группа Н существует на самом деле, но невозможно выявить конкретный способ определения, какие точки образуют эту группу. Иначе говоря, мы знаем, что группа Н существует, но не можем установить метод расчета точек, ее образующих.

Итак, должным образом комбинируя движения R и S, любой неаномальной точки сферы можно достичь из какой-либо точки группы Н. Заметим также, что поскольку точки группы Н неаномальны, то в результате применения к этим точкам различных последовательностей вращения всегда получаются разные результаты. Таким образом, для каждой неаномальной точки сферы Р есть только одна точка Q из группы Н и единственная комбинация движений R, S и N (записанная в сокращенной форме), которая ведет от Q до Р. (Как мы уже поясняли, возможно достигнуть Р из других точек Р’, которые не принадлежат группе Н, но это не имеет значения.)

В некоторых случаях комбинация движений, ведущих от Q до Р, будет движением 1-го типа; в других случаях — 2-го или 3-го. Назовем Нt группу, образованную всеми неаномальными точками сферы, которые получаются при применении движений 1-го типа; Н2 — образованную точками, которые получаются при применении движений 2-го типа, и Н3 — группу, образованную точками, которые получаются при применении движений 3-го типа.

Например, если Р — точка сферы, которая получается при применении вращения R к какой-то точке Q из группы Н, то есть если Р = (Q)R, то Р принадлежит Hv поскольку R — движение 1-го типа. Аналогично Р = (Q)RS принадлежит Н2, поскольку RS — движение 2-го типа, в то время как сама Q принадлежит Ну поскольку Q = (Q)7V, а N — движение 3-го типа. Из этого делаем вывод о том, что Нг содержит, в частности, все точки Н.

Вспомним, что, определенным образом комбинируя движения N, R и S, мы можем достичь любой (неаномальной) точки сферы из какой-либо точки группы Н, и так как все три типа включают в себя все возможные движения, делаем вывод, что Hv Н2 и Н3 вместе включают в себя все (неаномальные) точки шара. Можно сказать, что Hv Н2 и //3 — это три из восьми частей, на которые мы будем делить шар, чтобы построить из них два шара, равных исходному. Можно доказать, что на самом деле каждая из этих частей образована из несчетной группы радиусов шара, не связанных между собой; не будет ошибочным утверждать, что каждая из этих частей — это «несчетное облако отрезков». Наконец, заметьте, что Ну Н2 и Н3 сами по себе охватывают почти весь шар в том смысле, что невключенные точки занимают общий объем, равный нулю.

Если бы мы не исключили аномальные точки, различие между Ну Н2 и Н} было бы неоднозначным, поскольку существовали бы точки, принадлежащие одновременно двум или более частям. Предположим, что в группе Н была бы аномальная точка Q такая, как, например, (Q)RSS = (Q)SRS. RSS — движение 3-го типа, следовательно, Р = (Q)RSS принадлежала бы Ну но SRS — движение 2-го типа, следовательно, (Q)SRS, которая в действительности является той же самой точкой Р, также принадлежала бы и Нг Если исключить аномальные точки, можно избежать возникновения подобных ситуаций.

Ранее мы отметили, что целую часть как таковую характеризует тот признак, что все ее точки движутся синхронно. Также мы сказали, что движения, которые мы применим к частям шара, будут, по сути, комбинациями вращений R и 5. Итак, проанализируем, что происходит с Ну Н2 и Ну когда мы применяем к ним эти вращения.

Можно доказать, что если мы одновременно переместим все точки Ну применяя к ним вращение 5 (которое, как мы помним, является вращением на 120° вокруг D2), мы получим все точки Ну то есть, вращая согласно 5 часть сферы, которую мы назвали Ну мы получаем часть Ну Для того чтобы доказать это, нужно доказать, что если Р — точка группы Ну то (Р)5 — это всегда точка Ну а также что вращение Нг полностью покрывает Ну то есть любая точка Р’ из группы Н] получается вращением 5 какой-то точки из группы Н3 (это второе доказательство необходимо, чтобы оказалось ясным: движение //3 полностью покрывает Н3).

Итак, точки Н^ получаются применением движений 3-го типа к точкам Н; тогда, например, (Q)RSR и (Q)RSS обе принадлежат Н3 (где Q — одна из точек группы Н), поскольку RSR и RSS — движения 3-го типа. Заметим, что при применении вращения S к любой из этих двух точек мы получим в обоих случаях точки

из группы Ну Действительно, применив 5 к (Q)RSR, получим (Q)RSRS, которая принадлежит группе Ну поскольку RSRS — движение 1-го типа. То же самое происходит при применении 5 к (Q)RSS, так что мы получаем (Q)RSSS = (Q)R. Подводя итог:

RSR — движение 3-го типа —> RSRS — движение 1-го типа (по правилу 3).

(Q)RSR находится в Н3 —> (Q)RSRS находится в Ну

RSS — движение 3-го типа —» RSSS — R — движение 1-го типа (по правилу 1).

(Q)RSS находится в —> (Q)R находится в Ну

Эти примеры можно обобщить и таким образом доказать, как мы и утверждали ранее, что если Р находится в Ну то (Р)5 всегда находится в Ну

Что касается второй части доказательства, возьмем точку в группе Ну например (Q)S, где Q — точка в группе Н, и увидим, что она получается от вращения 5 точки в группе Ну Действительно, эта точка в группе Н3 и есть сама Q = (Q)/V. Очевидно, то же самое происходит, например, с точкой (Q)RSRS в группе Ну которая, как мы уже видели, является результатом вращения 5 точки (Q)RSR в группе Ну Эти примеры также можно обобщить, чтобы доказать, что при вращении Н3 мы покрываем, как и было сказано, все точки в группе Ну

Таким же образом можно доказать, что если мы применим вращение 55 к Н3 (оборот в 240° вокруг D2), получим Нг

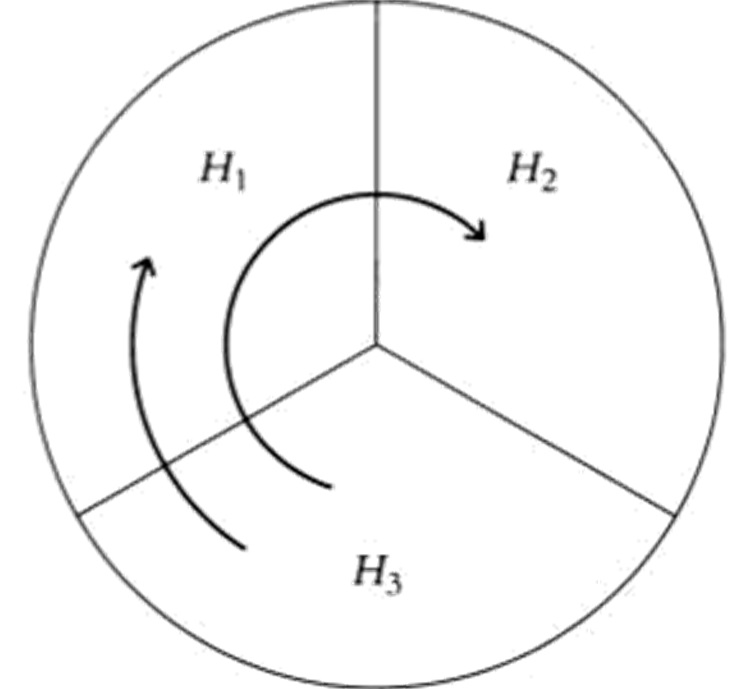
Подведем итог: если вращать часть Н} на 120° вокруг D2, мы получим Ну а если вращать ее на 240°, мы получим Нг На следующем рисунке схематически изображена эта ситуация.

Поскольку Н} и Н2 получаются из Нг одним простым вращением, можем ли мы

сделать вывод, что все три части имеют один и тот же объем? Так как Ну Н2 и /У3 вместе охватывают общий объем шара (поскольку у аномальных точек общий объем равен нулю), можем ли мы сделать вывод, что объем каждой из групп Ну Н2 и /У3 равен трети объема шара? Вернемся к этим вопросам в следующей главе.

Сейчас мы доходим до самой экстраординарной части доказательства, в которой мы по-настоящему удвоим объем. Мы увидели, что есть вращение (а именно 5), которое превращает /У3 в Ну и другое вращение (а именно 55), которое превращает /У3 в Нг Сейчас мы увидим, что движение R превращает /У3 в две другие части, //f и Н2, собранные в единое целое. То есть, вращая Н} согласно R, мы получаем одновременно /У, и Hy Если бы было верно, что у и Н2 тот же объем, что и у Ну то мы бы вращали Ну чтобы получить тело, имеющее вдвое больший объем.

Действительно, заметим, что если мы применим к Н3 вращение R (вращение на 180° вокруг оси север — юг), то получим точки как группы Ну так и Ну

RSS — движение 3-го типа —> RSSR — движение 1-го типа (по правилу 5).

(Q)RSS находится в /У? —> (Q)RSSR находится в Ну

RSR — движение 3-го типа —» RS — движение 2-го типа (по правилу 2).

(Q)RSR находится в /У3 —» (Q)RS находится в Нг

Эти примеры можно обобщить, чтобы показать: каждый раз, когда мы будем вращать согласно R точку из группы Ну мы получим точку /У( или точку Нг Другой пример — (Q)SR, которая находится в группе /У} и которая, если применить к ней движение R, дает в результате (Q)SRR = (Q)5 из группы /У, (Q — всегда точка группы /У); и еще один пример — (Q)SSR, которая также находится в /У3 и, если применить к ней движение R, дает в результате (Q)SSRR — (Q)55, находящуюся в группе Н2.

Точно так же можно доказать, что любой точки групп Иt и Н2 можно достичь с помощью вращения R точки из группы Ну Вращая /У3 согласно R, мы полностью покрываем вместе Н и Нг

Как такое возможно, что при вращении Нг получаются одновременно две остальные части? Представить эту ситуацию сложно. Но можно описать ее, отметив, что мы наблюдаем гигантский эффект отеля Гильберта, в котором каждый из радиусов, образующих Ну удваивается более или менее таким же образом, как в отеле могло поселиться бесконечное число новых постояльцев простым перемещением тех, кто уже был заселен.

Конец доказательства

Итак, мы разделили неаномальные точки сферы на три части, которые назвали Ну Н2 и Ну и мы знаем, что при применении вращения 5 к части Я3 получается Н,; что при применении вращения 55 к части Н} получается Н? и что при применении вращения R к части Н3 получаются Н] и Я7 одновременно.

Нг —» (вращение 5, 120° вокруг D7) —> Ну Н} —> (вращение 55, 240° вокруг D2) —> Я7.

/7} —» (вращение R, 180° вокруг D,) —> Я, + Нг

Можно сделать вывод, что при вращении //j на 120° вокруг D2 также получается Н2 (см. рисунок на стр. 77) и что в конечном счете Ну Н2 и могут быть получены друг из друга с помощью подходящих вращений; например, при вращении Я, на угол в 240° вокруг D2 получаем Ну.

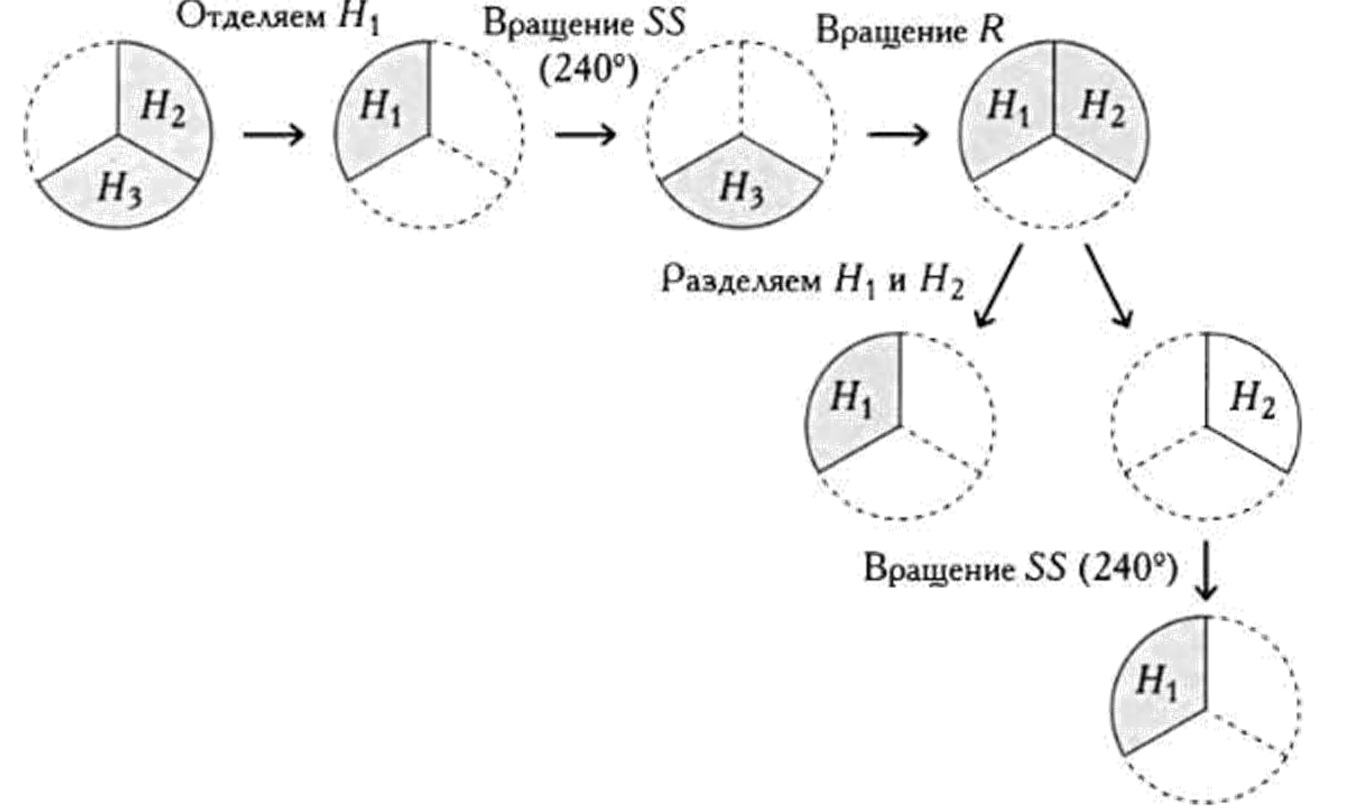
Теперь посмотрим, как мы можем удвоить неаномальные точки сферы. Чтобы удвоить Ну будем действовать, как показано на рисунке:

• шаг 1: переносим, не вращая, часть Ну чтобы отделить ее от шара;
•  шаг 2: вращаем Н^ согласно 55, чтобы превратить ее в Ну
• шаг 3: вращаем Н} согласно R, чтобы превратить ее в Н^ + Н2,
•  шаг 4: разделяем обе составляющие Н^ + Н2 (получаем копию Н^)’,
•  шаг 3: вращаем Н2 согласно 55, чтобы превратить ее в Нt (получаем вторую копию Н,).

С помощью перемещений и вращений мы превратили Н^ в Н} + Ну то есть удвоили часть Ну таким же образом мы можем удвоить Н7 и Ну В конце концов, получаем все три пары удвоенных частей и собираем из них два шара, равных исходному (кроме аномальных точек).

Что касается аномальных точек, можно доказать, что существует единственное вращение (отличное от 5, R или любой их комбинации), которое ставит их все одновременно внутрь области, охваченной Ну Н2 и Ну Это другая часть доказательства,

в которой (так же, как происходило с Н) утверждается существование некоего математического объекта, но нет никакого указания на то, как его получить. Доказательство того, что такое вращение существует, заключается в наблюдении, что общее число вращений, которые не ведут аномальные точки в область, охваченную Ну Н2 и Ну бесконечное, но счетное, в то время как общее число возможных вращений несчетное. Следовательно, должно существовать бесконечное число вращений, которые приводят аномальные точки в область, образованную Ну Н2 и Ну хотя мы и не можем указать ни одно такое вращение конкретно.

Итак, применяем ко всем аномальным точкам одновременно вращение, которое приводит нас в сектор шара, образованного Ну Н2 и Ну Аномальные точки разделены на пять частей, поскольку при правильном применении к ним вращений S и R они могут быть удвоены способом, не сильно отличающимся от того, что мы применили к Ну Н2 и Ну Таким образом, удвоение шара состоялось. Заметим, что именно на этом последнем шаге появляются пять дополнительных частей, которые в сумме с тремя указанными ранее и составляют восемь. Что и требовалось доказать.

Удивительное в теореме Банаха — Тарского заключается в том, что число частей, на которое разделен шар, конечное, но само это число неважно. Можно сказать, что с помощью различных движений можно добиться удвоения, используя пять частей вместо восьми, а также это можно сделать с четырьмя частями или меньше.

Можно доказать, что рассечением сферы на конечное число частей возможно собрать из этих частей сферу вдвое большего объема. К этой большей сфере также можно применить процесс удвоения, и так несколько раз. Таким образом, используя рассечение на конечное число частей, мы можем начать со сферы размером с виноградину и закончить сферой размером с Солнце, не добавляя материи ни на одном этапе.

Вывод:

Математика и физическая реальность

Можем ли мы разрезать шар из золота на восемь частей, чтобы собрать из них два шара, равных исходному? Или разрезать шар из золота, чтобы таким образом получить шар двойного объема? Кажется, что в теореме Банаха — Тарского утверждается, что это возможно, однако физика и здравый смысл отрицают шансы на такое удвоение материи. Как разрешить это противоречие?

Теорема Банаха — Тарского относится к математическому шару, то есть чисто абстрактному объекту, одна из характеристик которого заключается в том, что внутри него нет пустого пространства; каждая область, какой бы маленькой она ни была, содержит бесконечное число точек (и в доказательстве теоремы каждая из этих точек входит в состав либо Нг либо Н2, либо Ну или аномальна). Но мы не можем говорить о подобной заполненности точками настоящего, физического шара: если дотронуться до него, нам кажется, что он твердый, но на субатомном уровне шар почти полностью состоит из пустоты.

Следовательно, математический шар образован из бесконечного несчетного числа точек, и это принципиальное условие справедливости теоремы Банаха — Тарского,

но настоящий шар образован конечным числом атомов, следовательно, на нем нельзя воспроизвести процесс, описанный Банахом и Тарским.

Бесконечность — это математическая абстракция, которая не имеет соответствия в реальности. Точно так же в физической реальности не существует математических точек или отрезков с площадью, равной нулю, поскольку любой физический объект, даже самый маленький, имеет длину, ширину и высоту. И даже если одно из этих трех измерений окажется крошечным, оно все равно не будет равным нулю, поскольку не может быть меньше диаметра атома.

Вывод из этого состоит в том, что все способы разделить фигуры, тела или линии, в которых задействованы бесконечные части или такие объекты, как математические точки или отрезки, могут применяться только в абстрактном мире математики, но не в реальной жизни, где их место занимает деление, затрагивающее конечное количество многоугольников или криволинейных фигур.

И даже если допустить использование абстрактных частей, не существующих в физическом мире, теорема Банаха — Тарского не будет работать на плоскости. Невозможно разрезать круг или другую плоскую фигуру на конечное число частей (независимо от их природы) таким образом, чтобы получилось две фигуры, равных исходной. Эта невозможность была доказана Стефаном Банахом.

Стоит упомянуть, что современная физика вплотную подходит к отрицаемой Аристотелем актуальности бесконечности — то есть доступности в реальном мире, а не только в абстрактном. Например, есть понятие сингулярности, тесно связанное с чёрными дырами и теорией большого взрыва: это точка в пространстве—времени, в которой масса в бесконечно малом объёме сосредоточена с бесконечной плотностью. Уже есть солидные косвенные доказательства существования чёрных дыр, хотя теория большого взрыва находится ещё в стадии разработки.