Автор:
Гончарова Анастасия
Проблема:
Всегда ли простота означает изученность?
Цели исследования:
- Изучить историческое развитие простых чисел.
- Исследовать свойства простых чисел.
Задачи исследования:
- Найти и изучить теорию по этой теме.
- Изучить гипотезу Римана.
- Выяснить, существует ли самое большое простое число.
- Ознакомиться с методом «решето Эратосфена».
Актуальность проблемы:
Уже много тысячелетий, великие математики пытаются разгадать «загадку» простых чисел, ведь они все подчиняются закону, согласно которому, эти числа следуют друг за другом в определенном порядке. Его то как раз и не удалось найти и по сей день.
Гипотеза:
Если эти числа называются «простыми», то все эти числа давно изучены и про них уже все известно.
Методы исследования:
Теоретический анализ и обобщение научной литературы, использование материалов сети Интернет, опрос среди респондентов.
Этапы исследования:
- На первом этапе мы разобрали некоторые цели и задачи с помощью презентации
- Создали шкалу времени для рассмотрения истории развития простых чисел
- Посмотрели очень интересный ролик про числа, а также ролик, объясняющий на практике, что такое простые числа
- Cтатья про последние открытия в области современных чисел
- Нашли теорию по вопросу о существовании самого большого простого числа
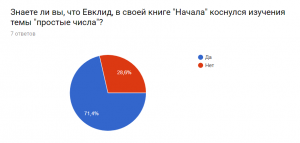
Древнегреческий математик Евклид занимался изучением простых чисел. В своей книге «Начала», он доказал, что простых чисел бесконечно много, т.е. за каждым простым числом есть еще большее простое число. Он вывел свою теорему о простых числах: «Первых простых чисел существует больше любого указанного числа их».
Доказательство: предположим, что существует некое наибольшее простое число P. Тогда перемножим все простые числа, начиная с 2 и кончая P, и увеличим полученное произведение на единицу: 2 3 5 7*… P + 1 = M. Если число М составное, то оно должно иметь по крайней мере один простой делитель. Но этим делителем не может быть ни одно из простых чисел 2, 3, 5, …, Р, поскольку при делении М на каждое из них получаем в остатке 1. Следовательно, число М либо само простое, либо делится на простое число, большее Р. Значит, предположение, что существует наибольшее простое число Р, наверно и множество простых чисел бесконечно.
Евклид доказал, что простых чисел бесконечного много. Можно сказать также, что среди простых чисел нет самого большого числа. Получается, что Евклид, уже больше двух тысяч лет назад лишил математиков надежды получить когда-нибудь полный список простых чисел. Много ученых пытались найти формулу для вычисления простых чисел, но у них ничего так и не получилось.
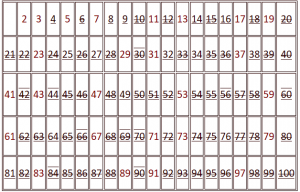
- Рассмотрели алгоритм нахождения простых чисел Эратосфена:
Предположим, что нам требуется найти все простые числа, лежащие на отрезке натурального ряда от 1 до некоторого числа N, например от 1 до 100. Способ исключения из этого промежутка всех составных чисел был известен еще греческому математику Эратосфену (276- 194гг. до н. э.) и носит название решето Эратосфена:
- Выписать все натуральные числа от 2 до N.
- Вычеркнуть 2 и далее каждое второе число, затем вычеркнуть 3 и каждое третье число.
- Продолжать этот процесс, пока возможно, выбирая всякий раз первое оставшееся не вычеркнутым число, следующее за тем, кратные которому были вычеркнуты последними.
- Числа, которые остались не вычеркнутыми, составляют множество всех простых чисел на отрезке от 1 до N.
Для N=100 имеем следующую таблицу:
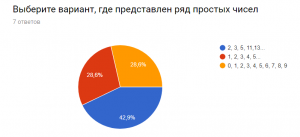
По результатам первого вопроса мы видим, что большая часть респондентов ответила верно на поставленный вопрос.
Здесь мы видим, что большая часть опрошенных знает, что Евклид изучал простые числа.
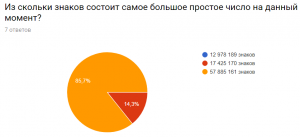
Анализируя третий вопрос, видно, что многие респонденты в курсе, из скольки знаков состоит самое большое число на сегодняшний день.
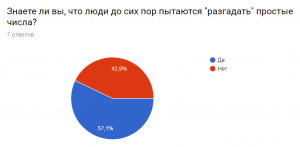
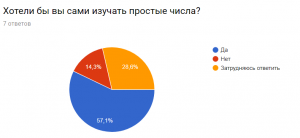
В этом вопросе мы видим, что мнения разделились, но большинство ответило «Да».
Из последнего вопроса мы узнаем, что респонденты хотели бы изучать простые числа, им это интересно.
Итог опросника: люди, не интересующиеся математикой все равно хотели бы изучать простые числа. Также мы узнали, что они все-таки хоть что-то знают из этой темы.
Вывод:
Действительно, как мы выяснили в ходе исследования, узнать всю необходимую нам информацию о простых числах нам не удалось и по сей день. Гипотеза опровергнута, «простые» числа на самом деле «сложные».