Актуальность темы «Простые числа. Долгая дорога к бесконечности» можно рассмотреть с нескольких точек зрения:
- Основы математики: Простые числа являются фундаментальными элементами теории чисел. Они играют ключевую роль в различных областях математики и служат строительными блоками для всех натуральных чисел.
- Современные технологии: Простые числа имеют важное значение в криптографии, особенно в алгоритмах, использующих факторизацию больших чисел. Это делает их актуальными в контексте безопасности данных и защиты информации.
- Исследования и открытия: Несмотря на то что простые числа изучаются уже много веков, в математике все еще существуют неразрешенные проблемы и гипотезы, такие как Гипотеза Римана, которые связаны с распределением простых чисел. Это делает тему актуальной для исследователей.
- Интерес широкой аудитории: Простые числа вызывают интерес не только у математиков, но и у широкой публики. Они часто становятся темой обсуждений в популярных научных книгах, статьях и лекциях.
- Образование: Изучение простых чисел помогает развивать логическое мышление и навыки решения проблем у студентов, что делает эту тему важной в образовательных программах.
Таким образом, тема «Простые числа. Долгая дорога к бесконечности» остается актуальной как в теоретическом, так и в практическом плане, открывая новые горизонты для исследований и применения в реальной жизни.
Прежде чем ознакомимся с данным проектом, предлагаю Вам посмотреть Тизер :
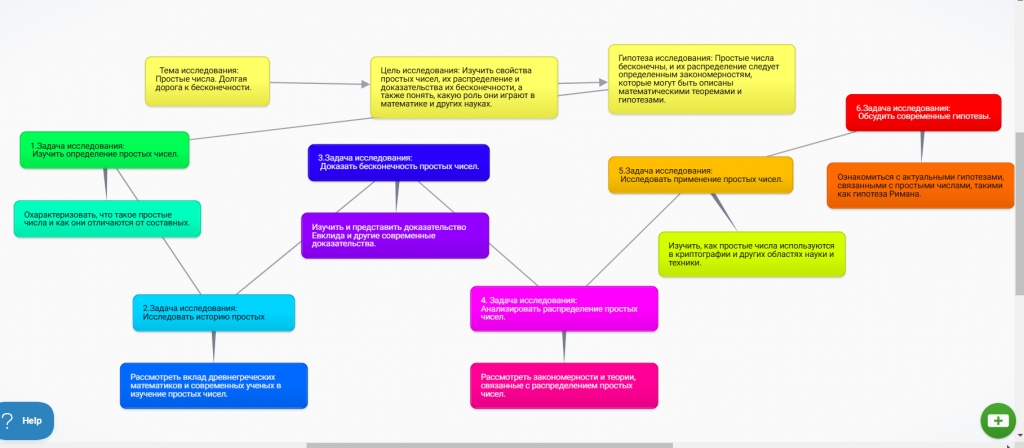
Цель исследования
Изучить свойства простых чисел, их распределение и доказательства их бесконечности, а также понять, какую роль они играют в математике и других науках.
Гипотеза исследования
Простые числа бесконечны, и их распределение следует определенным закономерностям, которые могут быть описаны математическими теоремами и гипотезами.
Задачи исследования
1. Изучить определение простых чисел: Охарактеризовать, что такое простые числа и как они отличаются от составных.
2. Исследовать историю простых чисел: Рассмотреть вклад древнегреческих математиков и современных ученых в изучение простых чисел.
3. Доказать бесконечность простых чисел: Изучить и представить доказательство Евклида и другие современные доказательства.
4. Анализировать распределение простых чисел: Рассмотреть закономерности и теории, связанные с распределением простых чисел.
5. Исследовать применение простых чисел: Изучить, как простые числа используются в криптографии и других областях науки и техники.
6. Обсудить современные гипотезы: Ознакомиться с актуальными гипотезами, связанными с простыми числами, такими как гипотеза Римана.
Методы исследования
1. Литературный обзор: Изучение книг, статей и научных публикаций по теории чисел и простым числам.
2. Анализ исторических источников: Исследование работ Евклида и других математиков, чтобы понять развитие идей о простых числах.
3. Экспериментальные методы: Опрос ,статистическая обработка результатов, анализ мнений участников
4.Обсуждение современных гипотез: Анализ текущих исследований и обсуждение гипотез с использованием доступных данных.
Историческая хронология событий
Исследование
Полный план проекта:
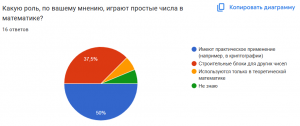
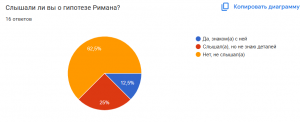
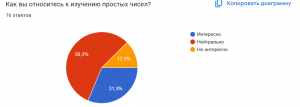
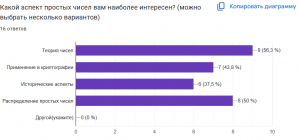
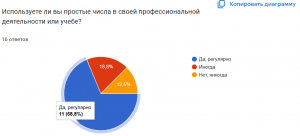
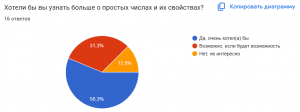
Опрос для респондентов по данной теме:
Этот опрос можно использовать для сбора мнений и уровня знаний респондентов о простых числах, а также для выявления интересов и предпочтений в данной области.
Интересные и курьезные факты
1. Бесконечность простых чисел: Первое доказательство бесконечности простых чисел было предложено Евклидом в III веке до н.э. Он доказал, что если взять любое конечное множество простых чисел и умножить их, добавив единицу, то результат не будет делиться ни на одно из этих простых чисел, что означает наличие хотя бы одного нового простого числа.
2. Число 2 — единственное четное простое: Все остальные четные числа делятся на 2 и, следовательно, не могут быть простыми. Это делает 2 уникальным среди простых чисел.
3. Гипотеза Римана: Эта гипотеза, предложенная Бернардом Риманом в 1859 году, касается распределения простых чисел и остается одной из самых известных нерешенных проблем в математике. Она утверждает, что все ненулевые нули дзета-функции имеют действительную часть 1/2.
4. Простые числа в природе: Некоторые исследователи заметили, что простые числа могут встречаться в природе, например, в циклах жизни некоторых насекомых (например, цикад), которые появляются через 13 или 17 лет — оба числа являются простыми.
5. Теорема о распределении: Простые числа распределены неравномерно; чем больше мы движемся по числовой оси, тем реже встречаются простые числа. Тем не менее, существует формула (приблизительная) для оценки количества простых чисел до заданного числа, известная как «теорема о распределении простых».
6. Простые числа и искусство: Некоторые художники и писатели вдохновлялись простыми числами. Например, американский писатель Джон К. Кэри написал роман «Простые числа», который исследует взаимосвязь между математикой и человеческими эмоциями.
Эти факты подчеркивают не только математическую важность простых чисел, но и их удивительное присутствие в различных аспектах науки и искусства!
Выводы:
Используемые источники
1. «The Prime Numbers and Their Distribution» — R. C. Baker, G. S. Harman, and J. L. Hensley
2. «Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics» — John Derbyshire
3. «Introduction to the Theory of Numbers» — G. H. Hardy и E. M. Wright
4. «The Music of Primes: Searching to Solve the Riemann Hypothesis» — Marcus du Sautoy
5. Wikipedia