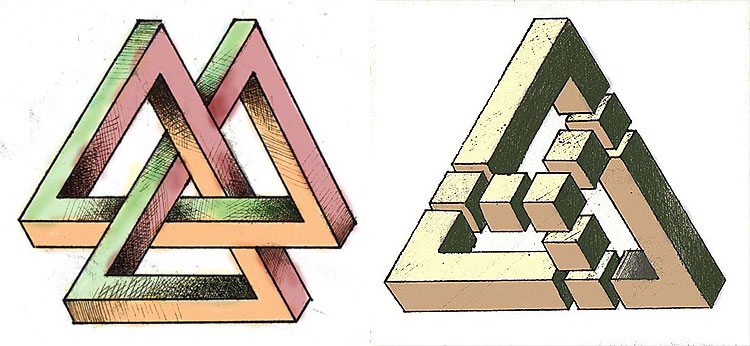Цель проекта:
1.Выяснить, как создаются невозможные фигуры и где их применяют.
Задачи проекта:
1.Изучить литературу по теме «Невозможные фигуры».
2.Составить классификацию невозможных фигур.
Тема работы актуальна ведь понимание парадоксов является одним из признаков того вида творческого потенциала, которым обладают лучшие математики, ученые и художники. Многие работы с нереальными объектами можно отнести к «интеллектуальным математическим играм». Моделировать подобный мир можно только с помощью математических формул, человек представить его просто не в состоянии. И для развития пространственного воображения оказываются полезными невозможные фигуры. Человек неустанно мысленно создает вокруг себя то, что для него будет просто и понятно. Он даже не может себе представить, что некоторые объекты, окружающие его, могут быть «невозможными». На самом деле мир един, но рассматривать его можно с разных сторон.
1.Определение невозможных фигур
Невозможная фигура — один из видов оптических иллюзий, фигура, кажущаяся на первый взгляд проекцией обычного трёхмерного объекта, при внимательном рассмотрении которой становятся видны противоречивые соединения элементов фигуры[1].
Невозможные фигуры – это геометрически противоречивые изображения объектов, не существующих в реальном трёхмерном пространстве. Невозможность возникает из противоречия между подсознательно воспринимаемой геометрией изображённого пространства и формально-математической геометрией.
Невозможные фигуры разделяются на два больших класса: одни имеют реальные трехмерные модели, а для других такие создать невозможно.
Невозможные фигуры достаточно часто встречаются на древних гравюрах, картинах и иконах — в одних случаях мы имеем с явными ошибками передачи перспективы, в других — с умышленными искажениями, обусловленными художественным замыслом.
В средневековой японской и персидской живописи невозможные объекты являются неотъемлемой частью восточного художественного стиля, дающего лишь общий набросок картины, детали которой «приходится» додумывать зрителю самостоятельно, в соответствии со своими предпочтениями [2].
Картины с искаженной перспективой встречаются уже в начале первого тысячелетия. На миниатюре из книги Генриха II, созданной до 1025 года и хранящейся в баварской государственной библиотеке в Мюнхене, нарисована «Мадонна с младенцем» (рис.1). На картине изображен свод, состоящий из трех колонн, причем средняя колонна по законам перспективы должна располагаться впереди Мадонны, но находится за ней, что придает картине эффект нереальности.
Рисунок 1. «Мадонна с младенцем»
2.Виды невозможных фигур
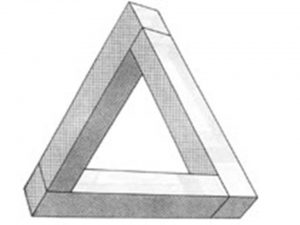
- Удивительный треугольник – трибар (рис.2).
Рисунок 2. Трибар
Эта – фигура – возможно первый опубликованный в печати невозможный объект. Она появилась в 1958 году. Её авторы, отец и сын Лайонелл и Роджер Пенроузы, генетик и математик соответственно, определили этот объект как «трехмерную прямоугольную структуру»[2]. Она также получила название «трибар». С первого взгляда трибар кажется просто изображением равностороннего треугольника. Но стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В тоже время левая и правая грани внизу тоже кажутся перпендикулярными. Если смотреть на каждую деталь отдельно, то она кажется реальной, но, в общем, эта фигура существовать не может. Она не деформирована, но при черчении были неправильно соединены правильные элементы.
Вот еще несколько примеров невозможных фигур на основе трибара (рис.3-6).
Рисунок 3. Тройной деформированный трибар
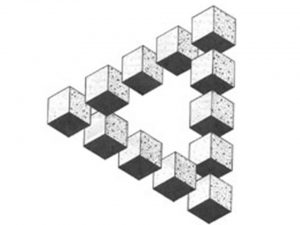
Рисунок 4. Треугольник из 12 кубов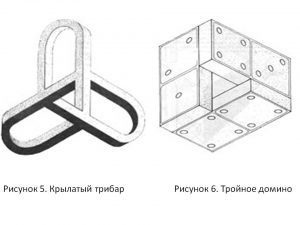
- Бесконечная лестница
фигуру чаще всего называют «Вечной лестницей» или «Лестницей Пенроуза» – по имени ее создателя. Ее также называют «непрерывно восходящей и нисходящей тропой» 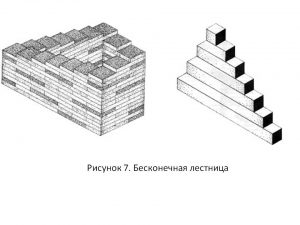
Впервые эта фигура была опубликована в 1958 году [2]. Перед нами предстает лестница, ведущая, казалось бы, вверх или вниз, но при этом, человек, шагающий по ней, не поднимается и не опускается. Завершив свой визуальный маршрут, он окажется в начале пути.
«Бесконечной лестницей» с успехом воспользовался художник Мауриц К. Эшер, на этот раз в своей литографии «Восхождение и нисхождение», созданной в 1960 году.
Лестница с четырьмя или семью ступеньками. На создание этой фигуры с большим количеством ступенек автора могла вдохновить куча обыкновенных железнодорожных шпал. Собравшись взобраться на эту лестницу, вы будете стоять перед выбором: подняться ли по четырем или по семи ступенькам.
- Космическая вилка
Следующая группа фигур под общим названием «Космическая вилка». С этой фигурой мы входим в самую сердцевину и суть невозможного. Может быть, это самый многочисленный класс невозможных объектов (рис.8).
Рисунок 8. Космическая вилка
Этот пресловутый невозможный объект с тремя (или с двумя?) зубцами стал популярен у инженеров и любителей головоломок в 1964 году. Первая публикация, посвященная необычной фигуре, появилась в декабре 1964 года. Автор назвал ее «Скобой, состоящей из трех элементов».
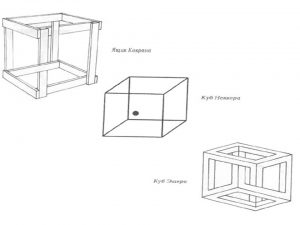
- Невозможные ящики
Еще один невозможный объект появился в 1966 году в Чикаго в результате оригинальных экспериментов фотографа доктора Чарльза Ф. Кокрана. Многие любители невозможных фигур проводили эксперименты с «Сумасшедшим ящиком». Первоначально автор назвал ее «Свободным ящиком» и заявил, что она была «сконструирована для пересылки невозможных объектов в большом количестве»(рис.9).
Рисунок 9. Невозможные ящики
2.Применение невозможных фигур
Невозможные фигуры находят иногда неожиданное применение. Оскар Рутерсвард рассказывает в книге «Omojliga figurer» об использовании рисунков имп-арта для психотерапии [3]. Он пишет, что картины своими парадоксами вызывают удивление, заостряют внимание и желание расшифровать. Психолог Роджер Шепард использовал идею трезубца для своей картины невозможного слона.
В Швеции их применяют в зубоврачебной практике: рассматривая картины в приемной, пациенты отвлекаются от неприятных мыслей перед кабинетом стоматолога.
За рубежом, на улицах городов, мы можем увидеть архитектурные воплощения невозможных фигур.
В последнее время было создано несколько мини скульптур и объемных моделей невозможных фигур. Им даже поставлен памятник.
Треугольник Пенроуза увековечен в городе Петре в Австралии. Он был установлен в 1999 году и теперь все, проходя мимо, могут увидеть невозможную фигуру (рис. 10).
Рисунок 10. Треугольник Пероуза в Австралии
.Невозможные фигуры в живописи
В живописи существует целое направление, которое называется импоссибилизм («невозможность») – изображение невозможных фигур, парадоксов. Интерес к импоссибилизму разгорелся к 1980 году. Этот термин был введен в обращение Тедди Бруниусом, профессором искусствоведения копенгагенского университета. Термин этот точно определяет то, что входит в это новое понятие: изображение предметов, которые кажутся реальными, но не могут существовать в физической реальности.
Фрактальная геометрия изучает закономерности, проявляемые в структуре природных объектов, процессов и явлений, обладающих явно выраженной фрагментарностью, изломанностью и искривленностью.
Оп-арт (англ. Op-art – сокращенный вариант optical art – оптическое искусство) – художественное течение второй половины 20 века, использующее различные зрительные иллюзии, основанные на особенностях восприятия плоских и пространственных фигур. Самостоятельным направлением в оп-арте является так называемый имп-арт (imp-art), использующее для достижения оптических иллюзий особенности отображения трёхмерных объектов на плоскости.
Наиболее известными представителями оп-арте являются Морис Эшер, венгерский художник Иштван Орос, фламандский художник Жос Де Мей, швейцарский художник Сандро дель Пре. Британский художник Джулиан Бивер – один из самых известных художников этого направления, который изображает свои шедевры не на бумаге, а на улицах города, стенах городских домов, где ими могут любоваться все.
- Невозможные фигуры в оформительском искусстве
Не редко невозможные фигуры используются для оформления обложек журналов.
Учебник по алгебре для 7 класса (рис.11).
Список литературы
- Левитин Карл Геометрическая рапсодия. — М.: Знание, 1984, -176 с.
- Пенроуз Л., Пенроуз Р. Невозможные объекты, Квант, № 5,1971, с.26
- Реутерсвард О. Невозможные фигуры. – М.: Стройиздат,1990, 206 с.
- Ткачева М.В. Вращающиеся кубики. – М.: Дрофа, 2002. – 168 с.
- Интернет ресурсы: